Zona prismei triunghiulare la o bază poligonală

Alte prisme diferite una de alta. În același timp, ele au multe în comun. Pentru a găsi aria bazei prismei, trebuie să înțeleagă ce fel este.

teoria generală

Prism este orice poliedru, din care părțile au forma unui paralelogram. În acest caz, baza sa poate fi orice polytope - din triunghiul la gon n. Care baza prismei sunt întotdeauna egale între ele. Asta nu se aplică părțile laterale - acestea pot varia foarte mult în dimensiune.

În rezolvarea problemelor întâlnite nu numai zona bazei prismei. Aceasta poate necesita cunoașterea suprafeței laterale, adică, toate fețele care nu sunt baze. Suprafața totală trebuie să fie unirea tuturor fețelor care alcătuiesc prisma.

Uneori înălțimea apare probleme. Este perpendicular pe bază. Diagonală a poliedru este un segment care face legătura între oricare două noduri de perechi care nu fac parte din aceeași față.

Trebuie remarcat faptul că aria bazei unei prisme drepte sau înclinat independent de unghiul dintre ele și fețele laterale. Dacă ei au aceeași formă la fețele de sus și de jos, zonele lor sunt egale.

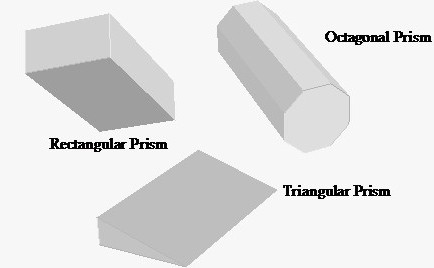
prisme triunghiulare

Este la baza figurii având trei noduri, care este un triunghi. El este cunoscut a fi diferit. Dacă triunghiul este dreptunghiular, este suficient să ne amintim că zona definită de picioare jumătate din muncă.

Expresia matematică este după cum urmează: S = ½ av.

Pentru a găsi zona unei baze prisme triunghiulare, în forma sa generală, formulă utilă Heron și una în care mâna este luată jumătate din înălțimea realizată la acesta.

Prima formulă va fi scrisă ca: S = √ (p (p-well) (p-c) (p-c)). semiperimetrul (p) este prezentă în înregistrare, adică suma celor trei laturi, împărțit la doi.

În al doilea rând: S = ½ * și pe.

În cazul în care este necesar pentru a afla prisme triunghiulare, amprenta la sol, care este corectă, atunci triunghiul este echilateral. Pentru aceasta are propria sa formula: S = ¼ și 2 * √3.

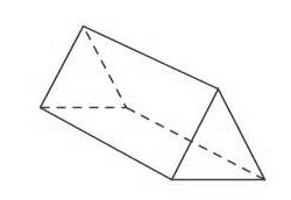
prismă patrulateră

Baza sa este oricare dintre dreptunghiuri cunoscute. Acest lucru poate fi un dreptunghi sau un pătrat, romb, sau o cutie. În fiecare caz, pentru a calcula aria bazei prismei, acesta va avea nevoie de propria lor formulă.

Dacă substratul - un dreptunghi, suprafața sa este definită ca: S = Av, unde A și B - dreptunghiului.

Când este vorba de o prisma patrulateră, suprafața corespunzătoare bazei prismei este calculată cu formula pentru un pătrat. Pentru că asta e ceea ce se dovedește a fi situată în partea de jos. Și S = 2.

În cazul în care baza - este o cutie, va avea nevoie de o astfel de ecuație: S = a *. Se întâmplă că partea de cutie și sunt unul dintre colțuri. Apoi, pentru a calcula înălțimea de necesitatea de a folosi formula suplimentară: a = în * sin A. Mai mult decât atât, unghiul A este adiacent la partea „b“ și o înălțime pe partea opusă unghiului respectiv.

Dacă baza prismei este un romb, apoi pentru a determina zona sa va avea nevoie de aceeași formulă ca cea a unui paralelogram (așa cum este cazul său). Dar puteți utiliza, de asemenea, acest lucru: S = ½ d1 d2. În cazul în care și d2 d1 - două diagonalelor unui romb.

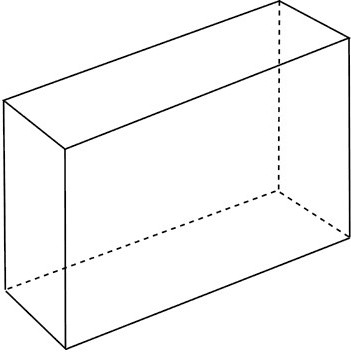
prismă pentagonal

Acest caz presupune descompunerea poligonului în triunghiuri ale căror zone sunt mai ușor de învățat. Deși se întâmplă ca cifrele pot fi un număr diferit de noduri.

Deoarece baza prismei - pentagon regulat, acesta poate fi împărțit în cinci triunghi echilateral. Apoi, suprafața de bază a prismei egală cu aria triunghiului (a se vedea formula de mai sus poate fi), înmulțit cu cinci.

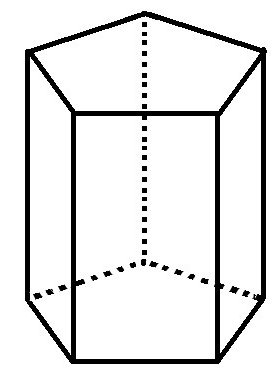
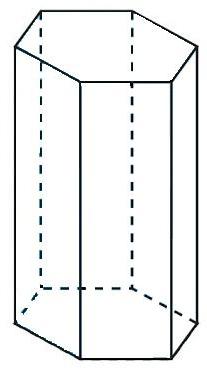
prismă hexagonală regulată

Conform principiului descris pentru o prismă pentagonală, este posibil să se rupă cu cap hexagonal de bază 6 triunghiuri echilaterale. Formula amprentei astfel de prismă similară cu cele anterioare. Numai în ea o zonă de triunghi echilateral ar trebui să fie înmulțită cu șase.

Uite formula este astfel: S = 3/2 și 2 * √3.

Numărul 1. Dana dreapta drept prisme rectangulare. diagonală egală cu 22 cm, înălțimea polyhedron - 14 cm Calculați suprafața de bază prismă și întreaga suprafață ..

Decizie. baza de prismă este pătrată, dar partidul nu este cunoscută. Este posibil să se găsească valoarea diagonalei unui pătrat (x), care este asociat cu prismei diagonală (d) și înălțimea (n). x 2 = d 2 - N 2. Pe de altă parte, această bucată de „x“ este ipotenuza unui triunghi, a cărei latură picioare egal pătrat. Aceasta este x 2 = a 2 + și 2. Astfel, se dovedește că un 2 = (d 2 - n 2) / 2.

D înlocuitor numărul 22, și „n“ se înlocuiește cu valoarea sa - 14, se dovedește că parte a pieței este egală cu 12 cm Acum, doar să învețe Footprint: 12 * 12 = 144 cm 2 ..

Pentru a găsi zona întreaga suprafață, este necesar să se stabilească valoarea de două ori a bazei și cvadruple partea pătrată. Acesta din urmă este ușor de a găsi formula pentru dreptunghiului: multiplica înălțimea și spre baza poliedrului. 14 și 12 și anume, acest număr este egal cu 168 cm 2. Suprafața totală a suprafeței prismei este de 960 cm2.

Răspuns. Suprafața bazei prismei este 144 cm 2. Întreaga suprafață - 960 cm2.

Numărul 2. Dan regulate prisme triunghiulare. La baza este un triunghi cu latura de 6 cm față laterală diagonală este de 10 cm Calculați pătrat: .. O bază și o suprafață laterală.

Decizie. Deoarece prisma este corectă, atunci baza sa este un triunghi echilateral. Prin urmare, o suprafață de 6 este egal cu patrat, înmulțită cu ¼ și rădăcina pătrată a 3. Un calcul simplu dă rezultatul: 9√3 cm 2. Această zonă a unei baze a prismei.

Toate fețele laterale sunt identice și reprezintă dreptunghiuri cu laturile 6 și 10 cm. Pentru a calcula aria suficientă pentru a se multiplica numerele. Apoi le înmulțește cu trei, pentru că fețele laterale în prisma atât de mult. Apoi, suprafața laterală a zonei plăgii este de 180 cm2.

Răspuns. Suprafață: Substrat - 9√3 cm suprafață laterală 2. prism - 180 cm2.

De ce să fie singur este bun pentru sănătate: 5 motive În societatea noastră, există un îndemn pe care oamenii se simt singuri proscriși mizerabile. Dar un psiholog de la Universitatea din California din Santa Barbara.