Provocări pentru dovada geometrică a faptelor de DPA

Propun acest timp pentru a aranja ceva de genul „dovezi-maraton“ pentru a aborda provocările cu care sunt oferite în variantele DPA elevii de clasa a IX-lea la matematică. Ele sunt asociate cu dovezi de simplu, dar în același timp, fapte geometrice foarte utile. Articolul în mod deliberat nu a furnizat o soluție detaliată a problemelor, doar câteva schițe și sfaturi. Încercați să depășească acest maraton de unul singur, fără erori și într-un du-te.

Problema 1. Demonstrați că mediatoare unghiurilor adiacente.

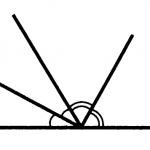
Unghiul α semnifică un arc, β - doi

Problema 2. Două segmente de curent alternativ și BD se intersectează într-un punct care este punctul de mijloc O. fiecare. Dovedește egalitatea ACD și triunghiuri CAB.

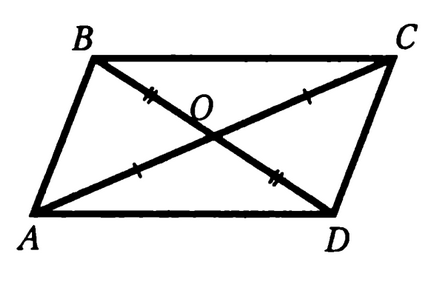
ABCD, desigur, este un paralelogram, dar cu condiția ca acest lucru nu este dat

Dovada: triunghiuri laterale sunt egale pe ambele părți și unghiul dintre ele (BO = OD - cu condiția ca, AO = OC - de stare, ∠DOC = ∠AOB - vertical), adică ∠ACD = ∠CAB. și pentru că acestea sunt situate transversal în AB directă. CD-uri și împărțit AC. atunci AB este paralela cu DC. În mod similar vom demonstra linii paralele BC și AD. Deci, ABCD - paralelogram prin definiție. BC = AD. AB = CD (în paralelogramul laturile opuse sunt egale), AC - totalul pentru ACD și triunghiuri CAB. astfel încât acestea sunt egale pe trei laturi. QED.

Problema 3. Arătați că mediana trase la baza unui triunghi isoscel, este bisectoarea unghiului substratului opus, și este perpendicular pe bază.

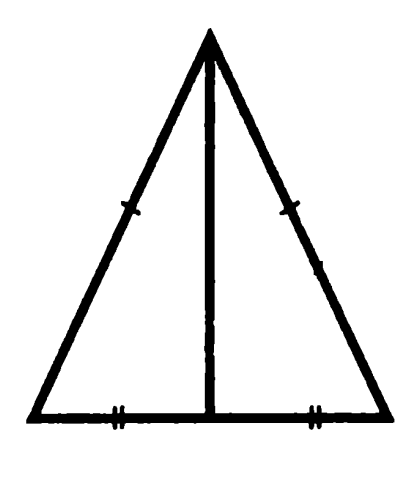
Unghiurile formate de mediana și baza, se numește „inferior“, mediane și laterale laturile - „superior“

Dovada: triunghiuri laterale în figură sunt pe trei laturi, din care egalitatea, în primul rând, unghiurile „superior“ (arătat că bisectoare), în al doilea rând, unghiurile „inferioare“, pentru a da suma ca adiacentă și egală cu 0. 180 cu toate acestea, pentru fiecare 90 0 (perpendicularitate prezentate). QED.

Problema 4. Demonstrați că mediana efectuat pe laturile unui triunghi isoscel sunt egale.

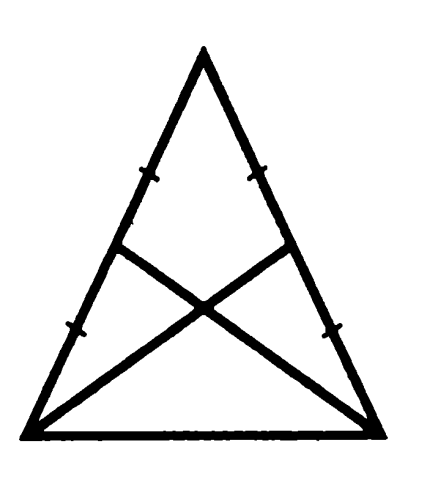
Triunghiuri medians formate, baze și jumătăți inferioare ale laturilor originale triunghi, numit „inferior“

Dovada: Unghiurile de la baza unui triunghi isoscel sunt egale, astfel încât triunghiurile „inferioare“ sunt egale pe ambele părți și unghiul dintre ele, ceea ce presupune egalitate a avut loc medianele. QED.

Problema 5. Demonstrați că bisectoarea trase din partea de sus a bazei unui triunghi isoscel sunt egale.

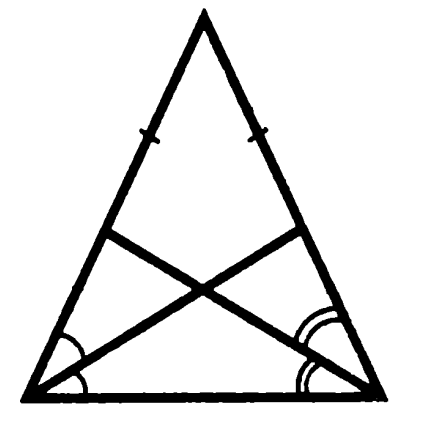
Toate unghiurile marcate în imagine, desigur, egal, deși, și sunt marcate cu arce

Dovada: „inferior“ triunghi este isoscel, după cum rezultă din egalitatea unghiurilor la fundul ei, „lateral“ triunghiuri laterale egale (egal dovedit mai sus particule Bisectors) și două unghiuri (primul egal în stare, acesta din urmă ca și verticală), astfel încât particulele Bisectoarele rămase De asemenea, egale între ele, și, astfel, ele însele sunt în întregime bisector. QED.

Problema 6. Demonstrați că lungimea segmentului care leagă mijlocul celor două părți ale unui triunghi este egală cu jumătate dintr-o terță parte.

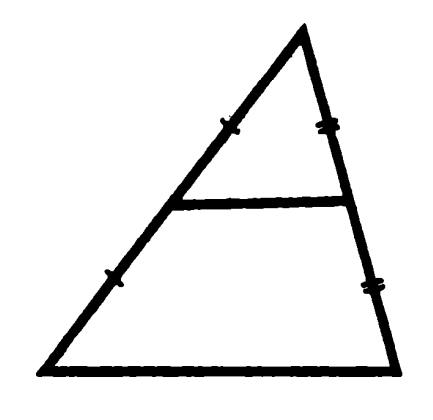
partea Neat se numește „baze“ a trecut - „Butoi“

Dovada: laturile triunghiului mici și mari din imagine este tratată ca 1, 2, în plus, ele au un unghi comun, astfel încât acestea sunt similare cu cea de a doua caracteristică cu factorul de similaritate 1, 2, și, prin urmare, baza sunt ambii 1 și 2. Că QED.

Problema 7. Demonstrați că diagonala unui paralelogram se împarte în două triunghiuri egale.

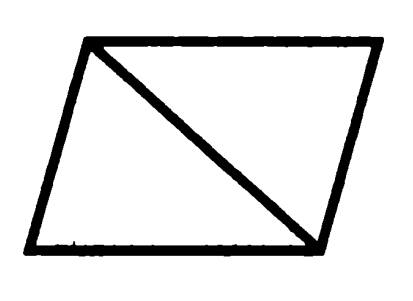
Paralelogram cu diagonala mai mult, probabil, nimic pentru a adăuga

Dovada: în părți opuse ale unui paralelogram sunt egale, diagonala este o parte comună a acestor triunghiuri, astfel încât acestea sunt egale pe trei laturi. QED.

Problema 8. Dovedește că mediana, triunghi dreptunghic trase la ipotenuzei este egal cu jumătate din ipotenuzei.

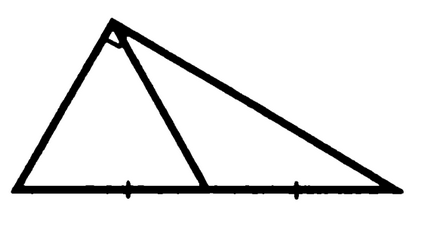
Cu alte cuvinte, mediana realizat din vârful unghiului drept

Dovada: în cazul în care în jurul unui triunghi dreptunghic dat pentru a descrie cercul, cercul înscris în unghiul drept al triunghiului va fi descris un semicerc, astfel încât ipotenuza este diametrul cercului, și jumătate din ipotenuza, și ne-a dat în problema mediana - razele, astfel încât acestea sunt toți egali. QED.

Sarcina 9. Demonstrați că segmentele unei tangente la circumferința de un punct, sunt egale.

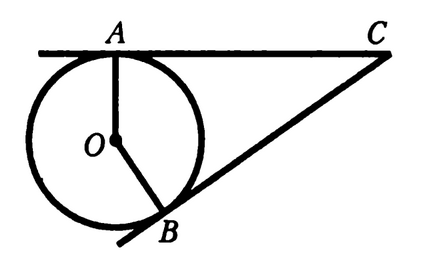
construcții suplimentare: conectați punctul C la punctul O (mental)

Dovada: unghiurile B și A linii (raze de cerc efectuat la punctul de oscilație perpendicular pe tangenta), înseamnă triunghiuri drept AOC și BOC sunt de-a lungul ipotenuzei (totalul pentru aceste contacte imaginar OC lateral) și un picior (un cerc cu raza OB = OA) și astfel AC = CB. QED.

Sarcina 10. demonstrează că diametrul care trece prin centrul cercului coardei este perpendicular pe ea.

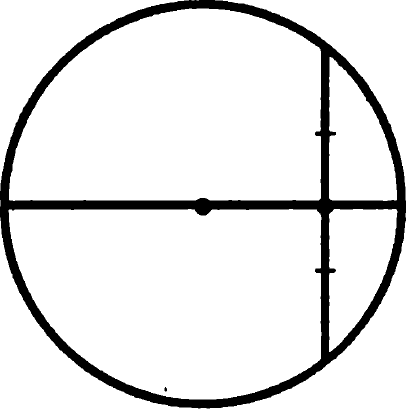
Linia care leagă cele două puncte în figură este mediana triunghiului, pe care o considerăm

Dovada: Într-un triunghi isoscel format de punctele de intersecție ale coardei cu cercul și centrul cercului descris mediana va fi mare, și, prin urmare, diametrul, care conține în sine înălțimea perpendiculară pe coardă. QED.

Sarcina 11. arată că în cazul în care cele două cercuri au o coardă comună, linia care trece prin centrul acestor cercuri perpendicular pe coardă dat.

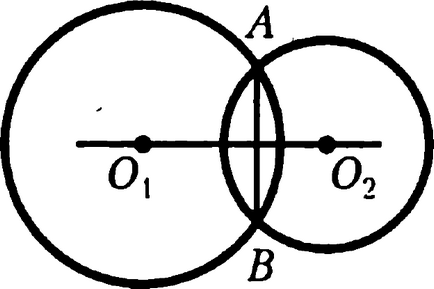
conectați Mental împreună toate punctele marcate în figură, punctul de intersecție se numește direcțiile orizontale și verticale H

Dovada: triunghiuri și O1AO2 O1BO2 sunt pe trei laturi, prin urmare, ∠HO2A = ∠HO2B. Apoi, triunghiuri HAO2 și HBO2 sunt egale pe ambele părți și unghiul dintre ele, atunci ∠AHO2 = ∠BHO2. și suma a două unghiuri egale poate da 180 0 numai când fiecare dintre ele este de 90 0. QED.

Sarcina 12. Arătați că, dacă un cerc poate fi înscris patrulater, suma lungimilor laturile opuse sunt egale.

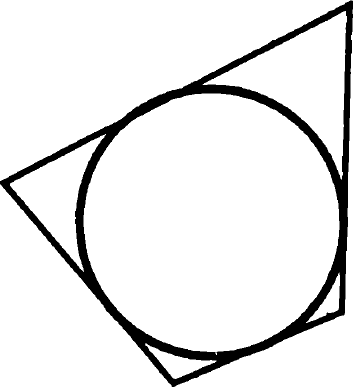
patrulater tangențiale. Sună-l ABCD. Fie M, E, X și L - punct de contact

Problema 13. Demonstrați că dacă unele dintre patrulaterului poate fi descris ca un cerc, atunci suma unghiurilor sale opuse sunt egale.

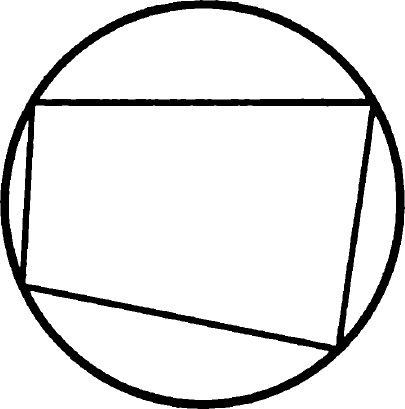
Dovada teoremei pe suma unghiului inscripționată unghiurilor opuse ale unui patrulater este de 180 0. împreună, deoarece ele se bazează pe un cerc complet, care măsoară 360 de grade 0. QED.

Problema 14. Demonstrați că, dacă unele dintre trapezului poate fi descris ca un cerc, trapezul isoscel.

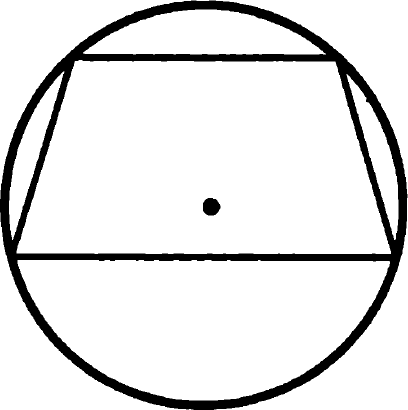
trapez isoscel înscris într-un cerc

Dovada: suma unghiurilor opuse ale unui patrulater înscris într-un cerc, este α + β = 180 0 (vezi sarcina 13.) Suma unghiurilor de la marginea trapezului, de asemenea, subunitatea egal + y = 180 0 (aceste unghiuri sunt fețe la bazele paralele și partea secantă side) de a compara aceste formule obținem că β = γ. adică, unghiurile de la baza unui trapez este egală, și este într-adevăr isoscel. QED.

Ținta 15. În pătrat punctul ABCD K și E - mijlocul laturile AB și, respectiv AD. Demonstrati ca este perpendicular pe KD CE.

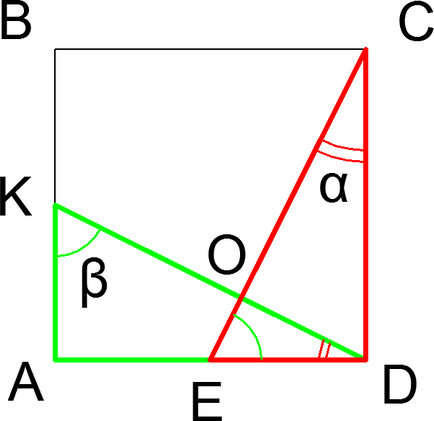
Imagine la sarcina

Dovada. Dreptul Triunghiuri AKD și DCE sunt două Catete, deci egal și toate elementele lor. lăsa

Suma unghiurilor într-un triunghi sunt egale în cazul în care, de exemplu, au AKD triunghi și, prin urmare, pentru triunghiul EOD au ceea ce este, și, prin urmare, ceea ce se dovedește perpendicular pe uscat și CE.

Dovedit fapte geometrice sunt importante, cunoștințele lor va fi un mare ajutor în rezolvarea problemelor mai complexe de geometrie, în primul rând de locuri de muncă C4 opțiune EGE în matematică. Prezentat aici explică soluțiile de referință care trebuie să fie puse în examen, desigur, nu sunt. Acestea sunt doar indicii, folosind care, cititorul va fi capabil să găsească o soluție pe cont propriu.

În orice caz, capacitatea de a rezolva probleme în geometria este o condiție esențială pentru obținerea unui scor mare la examen și GIA la matematică, care să garanteze accesul la mai multe universitati de prestigiu. Mult noroc pentru tine în curs de pregătire pentru GIA și utilizarea, profesori talentați și mult noroc în examen! tutorele tau Serghei V. geometrie.