Demonstrați că piciorul ipotenuza mai lung

Ipotenuzei unui triunghi dreptunghic este întotdeauna mai mare decât oricare dintre celelalte două părți. De ce? De fapt, ajunge la o astfel de concluzie poate fi de mai multe feluri.

În primul rând, dacă știți că, pe de altă parte, un unghi mai mare este întotdeauna o petrecere mare, și două triunghi dreptunghic unghi ascuțit indirectă, dovada va arata foarte simplu. Unghi drept este de 90 °, iar lângă ea se află ipotenuzei. unghiuri acute mai mici de 90 °, deci partea opusă lor (picioarele) este mai mic decât un unghi drept situată vizavi de ipotenuzei.

Dovada poate fi construit într-un mod diferit. Având în vedere un triunghi dreptunghiular ABC cu dreptul unghiului A. În acest caz, celelalte două părți sunt segmentele AB și AC, iar lungimea ipotenuzei BC.

Desenați-l pe segmentul de linie BC BD egal cu un picior AB.

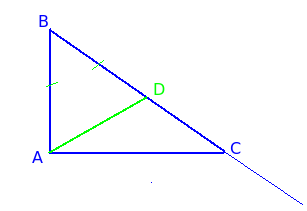
Dacă BC peste AB, punctul D este în afara ipotenuza BC, iar apoi piciorul peste ipotenuza. Dacă AB este mai mică decât BC, atunci punctul D se va afla în intervalul BC, ceea ce înseamnă mai puțin de piciorul ipotenuzei.

Luați în considerare triunghiul ABD. Acesta isoscel deoarece AB = BD prin construcție. După cum este cunoscut în triunghiuri isoscele unghiurile de bază sunt întotdeauna acute. Deci ∠BAD <∠BAC, так как ∠BAC прямой. Следовательно, луч AD лежит внутри угла ∠BAC и пересекает гипотенузу BC, то есть лежит на ней, а не за ее пределами. Поскольку доказано, что BD

În mod similar se poate demonstra că piciorul și ipotenuzei AC este mai mică decât BC, dacă vom construi un segment de CD, egal cu AC.

Aici isoscel ΔADC și ∠DAC <∠BAC. Следовательно луч AD лежит внутри ∠BAC и пересекает отрезок BC.