Conceptul triunghi și proprietăți

Decizia problemelor geometrice necesită o cantitate enormă de cunoștințe. Una dintre definițiile fundamentale ale acestei științe este un triunghi dreptunghic.

Conform acestui concept, se înțelege figura geometrică formată din trei colțuri și

părți, și magnitudinea unuia dintre unghiuri este de 90 de grade. Părțile care alcătuiesc unghiul drept sunt numite picioare, terțul, care i se opune, se numește ipotenuzei.

În cazul în picioare într-o figură egală, este numit un triunghi dreptunghic isoscel. În acest caz, există o afiliere la cele două tipuri de triunghiuri, ceea ce înseamnă că proprietățile observate în ambele grupuri. Reamintim că unghiurile de la baza unui triunghi isoscel sunt întotdeauna absolut, prin urmare, marginile ascuțite ale unei astfel de cifră ar include 45 de grade.

Prezența unuia dintre următoarele proprietăți sugerează că un triunghi dreptunghic este egal cu altul:

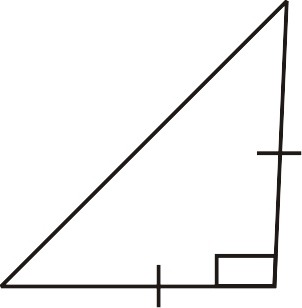
1. două picioare ale triunghiuri sunt egale;
2. Cifrele au aceeași ipotenuzei și unul dintre picioare;
3. sunt egale cu ipotenuza și orice colțuri ascuțite;
4. a observat starea de picior de egalitate și un unghi ascuțit.

Aria triunghiului dreptunghic este calculat ca ușor folosind formule standard, sau ca o cantitate egală cu jumătate din produsul din celelalte două laturi.

următoarele relații sunt observate în triunghiul dreptunghiular:

1. piciorul nu este nimic altceva decât media proporțională a ipotenuzei și proiecția acesteia pe ea;
2. în cazul în care pe cale de a descrie un cerc triunghi dreptunghic, centrul său va fi amplasat în mijlocul ipotenuzei;
3. înălțimea trase din unghiul drept este medie proporțională cu proiecțiile picioarele triunghiului de la ipotenuzei acestuia.

Interesant este faptul că, indiferent de triunghi dreptunghic, aceste proprietăți sunt întotdeauna respectate.

În plus față de proprietățile de mai sus caracteristice triunghiuri dreptunghiulare în următoarele condiții: pătratul ipotenuzei este egal cu suma pătratelor picioarelor.

Această teoremă este numit după fondatorul ei - teorema lui Pitagora. El a deschis acest raport angajate în studierea proprietăților pătratelor construite pe laturile unui triunghi dreptunghic.

Pentru a demonstra teorema vom construi un triunghi ABC, picioarele care notate a și b, și c ipotenuzei. În continuare, vom construi două pătrat. O parte va fi ipotenuzei, celelalte două picioare ale sumei.

Apoi, prima zonă a pieței pot fi găsite în două moduri: ca suma suprafețelor de patru triunghiuri ABC și al doilea pătrat, sau ca partea pătrată, desigur, că aceste raporturi sunt egale. Aceasta este:

4 cu 2 + (ab / 2) = (a + b) 2. transformă expresia rezultată:

2 +2 ab = a 2 + b 2 + 2 ab

Ca rezultat, obținem: c = a 2 + b 2 2

Astfel, figura geometrică ce corespunde unui triunghi dreptunghiular, nu numai toate proprietățile caracteristice ale triunghiurilor. Prezența unui unghi drept conduce la faptul că cifra are alte relații unice. Studiul lor va fi utilă nu numai în știință, ci și în viața de zi cu zi, ca o astfel de figură ca un triunghi dreptunghic se găsește peste tot.