Unghiurile înscrise într-un cerc

Unghiurile înscrise într-un cerc

Unghi împarte planul în două părți. Fiecare parte se numește un unghi plat. Figura 245 este umbrită unul din unghiurile plane cu laturile a și b. Unghiurile avion cu părțile comune se numesc complementare.

Dacă unghiul de plat face parte dintr-o jumătate de plan, atunci măsura de gradul de gradul este numit măsura unghiului convențional, cu aceleași părți. Dacă unghiul plan cuprinde o jumătate de plan, măsura de gradul este luată egală cu 360 ° - o unde o - măsură grade unghi plan suplimentar (246 Fig.).

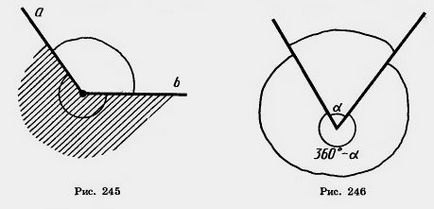
Unghiul central al unui cerc este numit un unghi de plat, în centrul său. Partea cerc situat în interiorul unghiului plan este numit arc de cerc care corespunde acestui unghi central (Fig. 247). Gradul de măsură cu arc numit masura gradul de unghi centrale corespunzătoare.

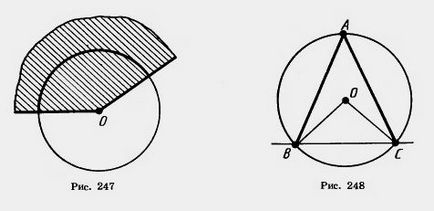
Unghiul al cărui vârf se află pe un cerc, iar laturile se intersectează acest cerc se numește un cerc înscris. Unghiul BAC 248 în figura înscrisă într-un cerc. Vârful său se află pe un cerc, iar laturile se intersectează cercul la punctele B și C. De asemenea, se spune că unghiul A se bazează pe coardă BC.

Sun Direct împarte cercul în două arce. Unghiul central de care corespunde uneia dintre aceste arce, care nu conține punctul A, numit unghiul centrală care corespunde acestui colț de înscris.

Teorema 11.5. Unghiul înscris într-un cerc, egal cu jumătate din unghiul centrală corespunzător.

Dovada. Considerăm mai întâi cazul particular în cazul în care una dintre laturile unghiului trece prin centrul cercului (Fig. 249 cat). Triunghiul AOB este isoscel, așa cum OA mână și OB sunt egale cu raze. Prin urmare, unghiurile A și B ale triunghiului sunt egale. Și, din moment ce suma lor este egală cu colțul exterior al triunghiului la vertex O, unghiul în triunghi este egal cu jumătate din unghiul AOC, după cum este necesar.

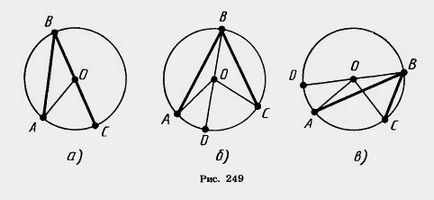
Cazul general, se reduce la cazul special al efectuării BD diametru auxiliar (Fig. 249, b, c). În cazul prezentat în Figura 249, b,

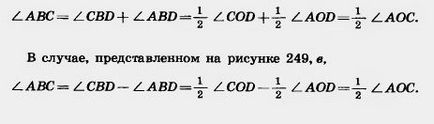
Teorema este demonstrată.

Teorema 11.5 implică faptul că unghiurile inscriptionate, laturile care trec prin punctele A și B din cerc, iar nodurile se află pe o parte a liniei AB sunt egale (Fig. 250).

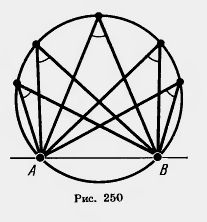
În special, unghiuri, în funcție de diametrul drepte.

A. V. Pogorelov, Geometrie pentru clasele 7-11, manual pentru instituțiile de învățământ

School Library on-line. manuale și cărți cu privire la toate disciplinele, matematică Grad 9 descărcare

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.