Un triunghi și un cerc

Cercul descris despre triunghiul se numește. dacă toate vârfurile triunghiului sunt situate pe cerc.

Centrul său echidistant față de toate nodurile, atunci trebuie să existe la punctul de intersecție al mediatoare laturilor triunghiului.

În consecință, cu privire la orice triunghi poate fi descris ca un cerc, de la mijlocul anilor perpendiculare pe lateral se intersectează la un moment dat.

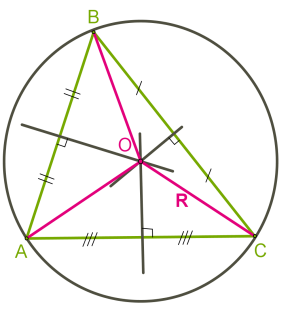
Pentru un triunghi înclinat acut este centrul cercului în triunghi.

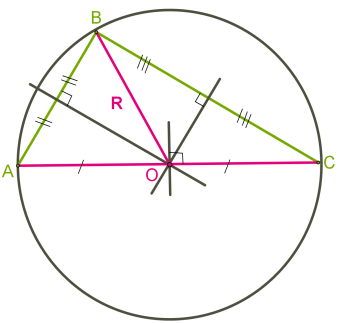
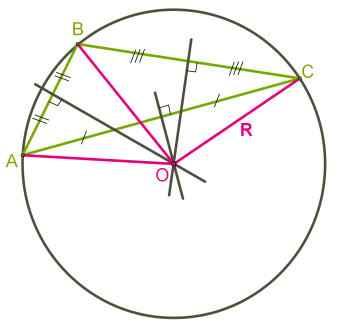
O altă situație cu triunghiuri dreptunghiulare și obtuze.

Un cerc înscris într-un triunghi

Un cerc înscris într-un triunghi se numește. în cazul în care toate laturile triunghiului atinge cercul.

Centrul său echidistant față de toate părțile, adică, trebuie să fie în punctul de intersecție al Bisectoarele triunghiului.

Prin urmare, în orice cerc triunghi poate fi înscris, ca bisectoarea triunghiului se intersectează la un moment dat.

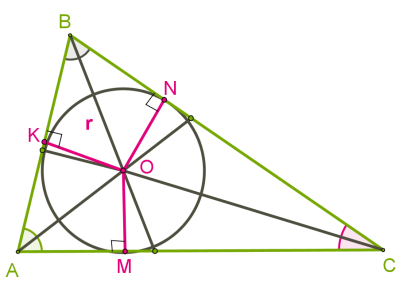
Deoarece bisectoarea unghiurilor unui triunghi se intersectează întotdeauna în interiorul triunghiului, centrul tuturor triunghiuri cerc înscris este în triunghiuri.

Într-un triunghi echilateral coincid bisectoare, medians și înălțimea, care este, de asemenea, aceste segmente sunt midperpendiculars. Acest lucru înseamnă că centrele de circumscrisă și cercul înscris de același.

Raza cercului circumscris

R = 03 februarie h. De aceea, R = 3 în martie.

Raza incircle

r = 1 3 ore. în cazul în care \ (h \) - înălțimea triunghiului.

Dacă este dat latura triunghiului \ (a \), atunci h = a2 în martie.

Prin urmare, r = 3 luna iunie

Raza cercului circumscris

R = 1 luna februarie c. unde \ (c \) - ipotenuza.

Raza incircle

r = S δ p. unde \ (p \) - semiperimetrul.

Raza cercului circumscris

R = un ⋅ b ⋅ c 4 ⋅ S δ

R = a 2 păcat α. unde α - unghi lateral opus \ (a \).

dacă S δ = abc 4 R. apoi R = abc 4 S δ; dacă S δ = p ⋅ r. atunci r = S δ p