Tipuri de matrice Matrici

Unitatea 1 Elemente de algebra liniara

Matricea, tipuri de matrici. Operații pe matrici. elemente de matrice. Matricea inversă

Definiție: Matricea se numește matrice dreptunghiular de numere compuse din m linii de lungime egală sau n coloane egal cu lungime.

aij - element de matrice, care este în primul rând i-lea și coloana j-a.

Principalele tipuri de matrice:

¾ pătrat (o matrice cu un număr egal de coloane și rânduri);

¾ transpun (pot fi obținute prin schimbarea rândurile și coloanele matricei în locuri O matrice de dimensiune pentru această transformare va fi dimensiunea matricei A T.);

¾ unitate (matrice pătratică, elementele diagonala principală care sunt egale cu unul, iar ceilalți sunt zero)

Matricile sunt utilizate pe scară largă în matematică pentru un sistem de înregistrare compact algebrice sau ecuații diferențiale liniare. În acest caz, numărul de rânduri ale matricei corespunde numărului de ecuații și numărul de coloane - numărul de necunoscute. Ca rezultat al sistemelor de ecuații liniare de rezolvare este redus la operații pe matrici.

Următoarele operații algebrice sunt definite pentru matricea:

¾ matrici de adiție cu aceeași dimensiune;

¾ multiplicare matrice de dimensiuni adecvate (o matrice având coloane se pot multiplica pe dreapta printr-o matrice cu rânduri);

¾ inclusiv multiplicarea cu un vector de matrice (de regula obișnuită de multiplicare matrice, vectorul este în acest sens cazul particular al matricei).

Luați în considerare operarea pe matrice cu mai multe detalii.

1. Adăugarea matricelor A + B este matricea C de a găsi operație, ale cărei elemente sunt suma pairwise tuturor elementelor relevante ale matricelor A și B, adică, fiecare element al matricei C egal cu

2. multiplice numărul matricei A # 955; (Simbol: # 955; A) este de a construi matricea B, ale cărui elemente sunt obținute prin înmulțirea fiecărui element al matricei A în această figură, adică fiecare element al matricei B este egal cu

3. Multiplicarea matrici (simbol: AB, cu semn de multiplicare mai mică) - este o operație de calcul al matricei C ale cărei elemente sunt egale cu suma produselor elementelor din linia corespunzătoare a primului multiplicator și a doua coloană (coloana multiplicare rând).

Numărul de coloane din matricea A trebuie să corespundă cu numărul de rânduri în matrice B. Dacă matricea A are dimensiune. matricea B -. atunci dimensiunea produsului AB = C este. A se vedea figura 1.

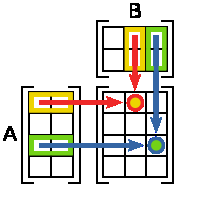
Figura 1 - Regula de înmulțire a două matrice

Exemplul 1: Găsiți A + 2B, în cazul în care. .

Exemplul 2: Find. în cazul în care.

Exemplul 3: Pentru a rezolva ecuația matrice :,

.

Definiție: Determinantul unei matrici A este notată: det (A) | A | sau # 916; A.

Formula de calcul determinant al doilea ordin:

Formulele pentru calcularea determinantului al treilea ordin:

a) extinderea elementelor prima linie:

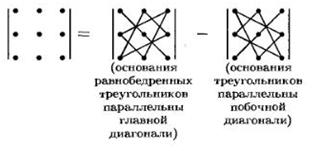
b) printr-o regulă asterisc (sau Sarryusa)

Proprietățile de bază ale determinanților.

Proprietatea 1. determinant nu este schimbat de transpunere, și anume

Notă. Următoarele proprietăți ale determinanților vor fi formulate numai pentru coarde. Atunci când această proprietate 1 implică faptul că aceleași proprietăți vor poseda și coloane.

Proprietatea 2. Atunci când înmulțirea elemente ale liniei determinant pentru un număr de determinantului este înmulțită cu acest număr, și anume

Proprietatea 3. Determinantul care are un șir de caractere nul este 0.

Proprietatea 4. factor determinant având două rânduri egale 0.

Proprietate 5. determinani două linii care sunt proporționale cu zero.

Proprietatea 6. Atunci când se deplasează cele două rânduri de determinant este înmulțită cu -1.

7. Valoarea de proprietate a determinantului nu se schimba în cazul în care elementele de un rând pentru a adăuga elemente corespunzătoare din alt rând înmulțit cu același număr.

8. Determinarea Minor care corespunde acestui element aij al determinant al treilea ordin, numit al doilea ordin determinant obținut cu anularea acestui rând și coloană la a cărui intersecție este elementul activ, adică rândul i-lea și coloana j-a. Minorii AIJ corespunzător acestui element va fi notat cu Mij.

Exemplul 4: minor M12. a12 elementul corespunzător. va fi determinant. care se obține prin anularea determinantul primul rând și a 2-coloană.

Definiția. Cofactor a determinantului elementului aij este numit minor Mij său. înmulțit cu (-1) i + j. Cofactor aij desemnează elementul Aij.

Din definiția observăm că relația algebrică dintre un element și complementul său este exprimată de minor Aij = (-1) i + j Mij.

Exemplul 5: Dan determinant. Găsiți A13. A21. A32.

Definiția. Dacă A - o matrice pătrată, matricea inversă este o matrice ea, notată cu A -1 și satisface condiția. (Se introduce această definiție, prin analogie cu numerele de multiplicare). Conceptul unei matrice inverse este introdusă numai pentru matrici pătrate.

Teorema. Pentru a matrice pătratică A avut opusul, este necesar și suficient ca determinant sa fie diferit de zero.

Deci, pentru a găsi este nevoie de inversa unei matrice:

1. Găsiți determinantul matricei A.

2. Găsiți matricea transpusa matricei rezultat.

3. Găsiți cofactori Aij elementelor matricei A și T compun o matrice ale cărei elemente sunt numerele Aij.

4. Se înmulțește matricea obținută în etapa 3

Exemplul 6: Găsiți inversa matricea A -1. dacă și validați.

. . Pentru a verifica formula utilizată. în cazul în care.