Soluție de ecuații trigonometrice
Bazat pe numele în sine arată că ecuația trigonometrice - aceasta este o ecuație în care necunoscutul se află sub semnul funcțiilor trigonometrice.
Sunt așa-numitele ecuații trigonometrice simple. Iată cum arată: Sinh = a, cos x = a, tg x = a. Să ia în considerare modul de a rezolva ecuații trigonometrice astfel. pentru claritate, vom folosi cercul trigonometrice acum familiare.

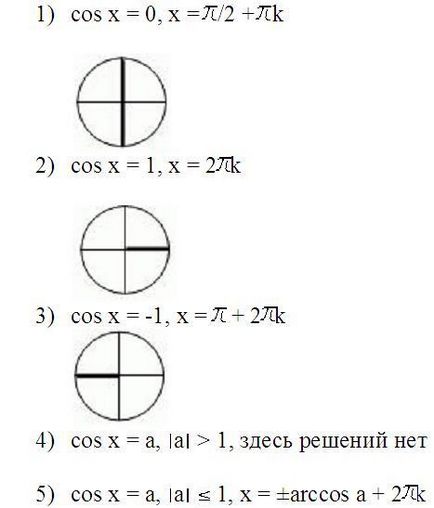
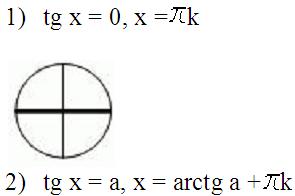
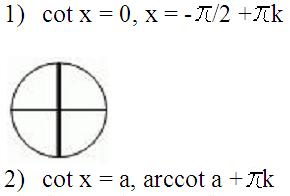
Orice ecuație trigonometrice este rezolvată în două etape: da ecuația la forma sa cea mai simplă și apoi a rezolva aceasta ecuatie trigonometrice la fel de simplu.
Există 7 metode principale prin care sunt rezolvate ecuațiile trigonometrice.
înlocuind metoda de substituție variabilă
Rezolva ecuația 2cos 2 (x + / 6) - 3sin (/ 3 - x) +1 = 0
Folosind formule de acționare se obține
2cos 2 (x + / 6) - 3cos (x + / 6) + 1 = 0
Înlocuiți cos (x + / 6) prin y pentru a simplifica și de a obține o ecuație pătratică obișnuită:
Rădăcini ale căror y1 = 1, y2 = 1/2
Acum du-te în ordine inversă
Substitut valorile obținute din y și obținem două opțiuni:
x1 = - / 2 + k 6x + / 6 = arccos ± 1/2 + k 2
x2 = ± / 3 - / 6 + k 2Soluție de ecuații trigonometrice prin factoring
Cum de a rezolva păcatul ecuația x + cos x = 1?
Se transferă toate stânga la dreapta a fost 0:
sin x + cos x - 1 = 0
Noi folosim cel discutat mai sus identități pentru a simplifica ecuația:
sin x - 2 păcat 2 (x / 2) = 0
Noi facem factorizarea:
2sin (x / 2) * cos (x / 2) - 2 păcat 2 (x / 2) = 0
2sin (x / 2) * [cos (x / 2) - sin (x / 2)] = 0
Obținem două ecuații
Această ecuație trigonometrică simplă a cărei soluție
x1 = 2 kAceastă ecuație este omogenă și poate fi rezolvată de către un al treilea, care va fi discutat mai jos.
ecuația Divizare în cos (x / 2) și de a obține din nou ecuația trigonometrice simplu:
x / 2 = arctg 1 + k
Reducerea ecuației omogene
Ecuația este omogenă în ceea ce privește sinus și cosinus, în cazul în care toți membrii săi cu privire la sinusul și cosinusul același grad de același unghi. Pentru a rezolva ecuația omogenă, se procedează după cum urmează:
a) transfera toți membrii săi în partea stângă;
b) să ia toate factorii comuni ai parantezele;
c) echivala toți factorii și paranteze la 0;
g) obținut în paranteze ecuație omogenă grad mai mic, acesta la rândul său, este împărțit de sinus sau cosinus, în cel mai înalt grad;
d) rezolvă ecuația rezultată pentru tg.
3sin rezolva ecuatia x + 2 sin x 4 • x + cos 5 cos 2 x = 2
Folosind formula păcatului 2 x + cos 2 x = 1 și a scăpa de două drept deschis:
3sin 2 x + 4 • sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x
păcatul 2 x + 4 • sin x cos x + 3 cos 2 x = 0
2 tg tg x + 4, x + 3 = 0
Înlocuiți tg x la y și a obține ecuația de gradul doi:
2 y + 4y +3 = 0, ale cărui rădăcini y1 = 1, y2 = 3
Prin urmare, vom găsi cele două soluții ale ecuației inițiale:
x2 = arctg 3 + k
Soluția de ecuații, prin trecerea de la o jumătate de unghi
Rezolva ecuatia 3sin x - 5cos x = 7
6sin (x / 2) * cos (x / 2) - 5cos 2 (x / 2) + 5sin 2 (x / 2) = 7sin 2 (x / 2) + 7cos 2 (x / 2)
Prerenosim toate stânga:
2sin 2 (x / 2) - 6sin (x / 2) * cos (x / 2) + 12cos 2 (x / 2) = 0
tg 2 (x / 2) - 3TG (x / 2) + 6 = 0
Ei bine, după modelul deja stabilit ...Introducere unghi auxiliar
Pentru a lua în considerare ecuația de forma: a sin x + b cos x = c,
unde a, b, c - unor coeficienți arbitrare și x - necunoscut.
Ambele părți ale divizate în:
Acum, ecuația coeficientii conform formulelor trigonometrice au proprietăți păcătuiesc și cos, și anume: modul lor de cel mult 1 și suma pătratelor = 1. le Notam respectiv ca cos si pacatul, unde - acesta este un unghi auxiliar așa-numitul. Apoi, ecuația devine:
cos * sin x + sin * cos x = C
Soluția acestei ecuații este trigonometric simplu
x = (-1) k * arcsin C - + k, în care
Trebuie remarcat faptul că desemnarea cos și a păcatului sunt interschimbabile.
Rezolva 3x ecuație păcat - cos 3x = 1
În această ecuație, coeficienții:
a =, b = -1, deci vom împărți ambele părți cu 2 =
(/ 2) * 3x sin - (1/2) cos 3x = 1/2
cos (/ 6) * 3x sin - sin (/ 6) * cos 3x = 1/2
x = (-1) k * / 18 + / 18 + k / 3Conversia la suma produsului
Aici, vom folosi doar formula trigonometrice
Rezolva ecuația 2 sin x * sin 3x = cos 4x
Transformarea în partea stângă, în valoare de:
cos 4x - cos 8x = cos 4x
Noi primim o ecuație simplă:
substituție universală
Pentru a rezolva ecuatia 3sin trigonometrice x - 4cos x = 3
Sunt 2 cazuri:
- x (2k + 1),
Apoi, folosind formulele trigonometrice, obținem:
3 [(2tg (x / 2)) / (1 + tg 2 (x / 2)] - 4 [(1 - tg 2 (x / 2)) / (1 + tg 2 (x / 2)] = 3
6TG (x / 2) - 4 + 4tg 2 (x / 2) = 3 + 3TG 2 (x / 2)
tg 2 (x / 2) + 6TG (x / 2) - 7 = 0
Efectuarea de înlocuire tg (x / 2) pentru a obține y și ecuația pătratică:
ale cărui rădăcini y1 = -7, y2 = 1
Ne întoarcem și să obțină două ecuații simple de:
x1 = -2arctg 7 + k 2
apoi 3sin [(2k + 1)] - 4cos [(2k + 1)] = 04 martie
Obținem - decizia este doar prima condiție.
Sunt binevenite orice întrebări.
Pentru mine, sinus și cosinus - aceasta este o pădure întunecată, pe care probabil voi fi niciodată capabil să depășească. Deși se pare că, uneori, chiar știu cum să rezolve ecuații trigonometrice. Încerc din nou pentru a re-citit articolul, pentru a înțelege.
Și totuși a rezolvat ecuatii trigonometrice prin metoda de substituție este mult mai dificil decât să se stabilească de factoring. Dar introducerea unui unghi de sprijin este prea fantastic pentru nivelul meu de elev.
Prefer doar pentru a rezolva ecuatii trigonometrice metoda de factoring.
Cu toate acestea, uneori, eu folosesc următoarea metodă pentru alinierea omogenă. Toate celelalte opțiuni, cum să rezolve ecuații trigonometrice, nu a fost încă pe deplin înțeles.
În ce momente ale vieții pot fi utile trigonometria? Și mă întreb, există o mai simplificate soluții suplimentare de ecuații trigonometrice? Aș spune pentru începători sau „Dummies“?
Am citit despre sinus și cosinus și a dat seama că din moment ce anii de școală nu este atât de mult, și totul sa schimbat. Pentru că în acel moment în mod similar, toate sa dovedit și acum exact același „cântec“. Pentru a rezolva ecuații trigonometrice nevoie pentru întreaga afacere bine.
De ce trigometricheskoe decizia trebuie să fie împărțită doar în două etape, și nu mai mult? Ar fi interesant încă într-un fel mai diferit toate divizat și să decidă decât doar pe unele standard, pe care le puteți modifica, probabil.
Nu înțeleg sensul primului exemplu, pare să fi găsit răspunsul și apoi se substituie după cum se menționează în sens opus. De ce face asta? Deci, ce a fost modificat pentru a avea în continuare trebuie să conducă la o decizie?!
Te rog spune-mi că ar putea fi un program care rezolva automat aceste ecuații vor fi.