Reprezentarea grafică a funcțiilor pătratice ale algoritmului și exemple
principal nbsp> nbsp Wiki-Tutorial nbsp> nbsp matematică nbsp> clasa nbsp9 nbsp> nbspPostroenie grafic funcții pătratice: algoritmul și exemple
O funcție pătratică este o funcție de forma:
y = a * (x ^ 2) + b * x + c,
în cazul în care un - coeficient de cel mai înalt grad de necunoscut x,
b - coeficientul pentru x necunoscut,
și - un membru gratuit.
Graficul curbei funcției pătratice este numită parabolei. Forma generală a parabolei este prezentată mai jos.
Figura 1. Vedere generală a parabolei.
Există mai multe metode diferite de reprezentarea grafică a unei funcții pătratică. Ne vom uita la bază și cele mai frecvente dintre ele.
Un algoritm pentru construirea graficului funcției pătratice y = a * (x ^ 2) + b * x + c
1. Construirea unui sistem de coordonate menționat interval unitate și semn axe de coordonate.
2. Se determină direcția ramurilor parabolei (în sus sau în jos).
Pentru a face acest lucru, uita-te la semnul coeficientului a. În cazul în care un plus - ramurile sunt îndreptate în sus, dacă este negativ - ramurile din partea de jos.
3. Se determină Coordonata x vârf al parabolei.
Pentru aceasta, utilizați formula Hvershiny = -b / 2 * a.
4. Se determină coordonatele la vârful parabolei.
Pentru aceasta substituit în ecuația Uvershiny = a * (x ^ 2) + b * x + c x în loc găsit în valoarea anterioară etapa Hvershiny.
5. Se aplică punctul rezultat pe programul și efectua aceasta prin axa de simetrie paralelă cu axa de coordonate y.
6. Găsiți punctul de intersecție al graficului cu axa x.
Acest lucru necesită rezolvarea ecuației pătratice a * (x ^ 2) + b * x + c = 0 una dintre metodele cunoscute. Dacă ecuația nu are rădăcini reale, atunci graficul funcției intersectează axa x.
7. Găsiți coordonatele punctului de intersecție al graficului cu axa y.
Pentru această valoare este substituită în ecuația x = 0 și se calculează valoarea lui y. Remarcăm acest lucru și un punct simetric pe grafic.
8. Găsiți coordonatele unui punct arbitrar A (x, y)
Pentru a face acest lucru, pentru a alege o valoare arbitrară a x coordonate, și înlocuiți-l în ecuația noastră. Obținem valoarea la acest punct. Aplicați un punct de pe grafic. De asemenea, notat pe grafic reflexia punctului A (x, y).
9. Conectați punctele obținute în linia lină grafic și continuă grafic pentru punctele finale până la sfârșitul axei de coordonate. Semnați programul sau pe balon, sau, în cazul în care spațiul permite, de-a lungul graficului în sine.
Exemplu de complot
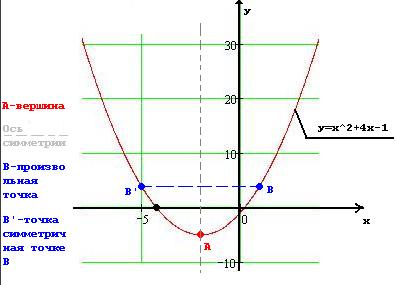
Ca exemplu, vom construi un grafic al funcției pătratică dată de ecuația y = x ^ 2 + 4 * x-1
1. Desenați axele de coordonate, le semneze și notați intervalul de unitate.
2. Valorile coeficienților a = 1, b = 4, c = -1. Deoarece a = 1, care este mai mare decât zero ramură parabole îndreptate în sus.
3. Determina x coordonata nodului parabolei Hvershiny = -b / 2 * A = -4 / 2 * 1 = -2.
4. Se determină coordonatele în vârful parabolei
Uvershiny = a * (x ^ 2) + b * x + c = 1 * ((- 2) ^ 2) + 4 * (- 2) - 1 = -5.
5. Nota de sus și mențineți axa de simetrie.
6. Găsiți pătrat punctului graficului de intersecție cu axa x. Rezolvarea ecuației pătratice x ^ 2 + 4 * x-1 = 0.
x1 = -2-√3 x2 = -2 + √3. Menționăm valorile obținute pe diagramă.
7. Găsiți punctul de programul de intersecție cu axa y.
x = 0; y = -1
8. Alegeți un punct B. arbitrar Să are coordonate x = 1.
Apoi, y = (1) ^ 2 + 4 * (1) -1 = 4.
9. Punerea punctelor obținute și programul de conectare.
Rezultatul va fi un program.