Pregătirea studenților pentru examenul și OGE (DPA), în rezoluția centru de formare (manual de matematică -
Perpendiculara pe segmentul de linie
1. Determinarea mediatoare segmentului se numește, o linie perpendiculară pe acest segment și care trece prin mijlocul ei (fig. 1).
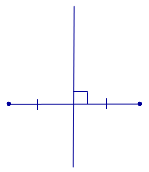
Teorema 1. Fiecare punct al perpendiculara pe segmentul se află la aceeași distanță de la capetele acestui segment.
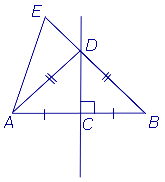
Dovada. Să considerăm un punct arbitrar D. situată pe perpendiculara AB (figura 2) segment, și demonstrează că ADC și BDC sunt triunghiuri.
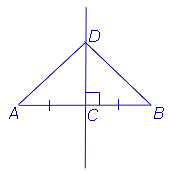
Într-adevăr, aceste triunghiuri sunt triunghiuri drepte ale căror picioare sunt AC și BC sunt egale, iar piciorul este comun DC. Din egalitatea ADC triunghiuri și BDC implică faptul că AD și segmentele DB. Teorema 1 este demonstrată.
Teorema 2 (inverse Teorema 1). Dacă punctul se află la aceeași distanță față de capetele segmentului, se află pe perpendicular pe acest segment.
Dovada. Dovedim teorema de 2 „din contra.“ În acest scop, să presupunem că un punct E este la aceeași distanță de la capetele segmentului, dar nu se află pe perpendicular pe acest segment. Să-l dea la o contradicție. Să considerăm mai întâi cazul în care punctele A și E se află pe laturile opuse ale perpendiculara (Figura 3). În acest caz, segmentul EA se intersectează perpendicular la un moment dat, care va fi notată cu litera D.
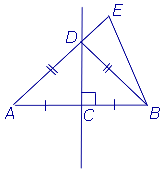
Vom demonstra că lungimea segmentului segmentului AE EB. De fapt,
Astfel, în cazul în care un punct de E și A se află pe laturile opuse ale perpendiculara, avem o contradicție.
Acum considerăm cazul în care un punct E și A se află pe o parte a perpendicularei (Figura 4). Vom demonstra că segmentul EB mai lung segment AE. De fapt,
Această contradicție completează dovada teoremei 2
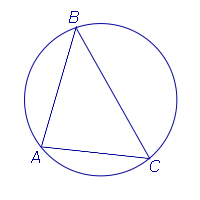
Circumscris triunghiului
2. Determinarea cercului circumscris despre triunghiul. Este cercul care trece prin toate cele trei vârfuri ale unui triunghi (Figura 5). În acest caz, triunghiul este numit un triunghi înscris într-un cerc sau un triunghi înscris.