Metode pentru sisteme de ecuatii rezolvare

Care sunt metodele de rezolvare a sistemelor de ecuații?

În această secțiune, vom discuta trei metode pentru sistemele de ecuații de rezolvare. mai fiabile decât metoda grafică, care a fost considerată în secțiunea anterioară.

metoda de substituție

Această metodă am folosit în clasa a 7-a pentru sistemele de ecuații liniare de rezolvare. Algoritmul care a fost dezvoltat în clasa a 7-a, este destul de potrivită pentru sistemele de ecuații de orice (liniar, nu neapărat), două cu două variabile x și y rezolvare (desigur, variabile pot fi definite și celelalte litere, nu contează). De fapt, acest algoritm am folosit în paragraful precedent, în cazul în care problema numărului de două cifre a condus la un model matematic, care este un sistem de ecuații. Acest sistem de ecuații de mai sus, am decis metoda de substituție (vezi. Exemplul 1 în § 4).

Un algoritm folosind tehnica de substituție pentru rezolvarea unui sistem de două ecuații în două variabile x și y.

1. Pentru a exprima în termeni de x al unui sistem de ecuații.
2. Substituind expresia y în cealaltă ecuație a sistemului.
3. Pentru a rezolva ecuația rezultată pentru x.
4. suplean alternativ fiecare dintre rădăcinile găsite de ecuația la a treia etapă, în locul lui x în y expresie prin x, obținut în prima etapă.
răspuns 5. Înregistrarea în formă de perechi de valori (x, y), care au fost găsite, respectiv, a treia și a patra etapă.

Variabilele x și y, desigur, drepturi egale, deci cu același succes putem, în prima etapă a algoritmului nu exprimă în termeni de x, y și x prin a unei ecuații. De obicei, alegeți ecuația care este mai simplu, și exprimă variabila din ea, pentru care procedura este mai simplă.

Exemplul 1 Pentru a rezolva sistemul de ecuații

1) exprimă x în ceea ce privește y din prima ecuație: x = 5 - 3y.
2) Substituind această expresie pentru x în a doua ecuație: (5 - 3 a) y - 2.
3) Rezolvăm ecuația rezultată.

4) Înlocuind alternativ fiecare dintre valorile obținute ale y în formula x = 5 - Zu. În cazul în care
5) cuplu (2; 1) și soluțiile sistemului de ecuații date.

Metoda algebrică plus

Această metodă, cum ar fi metoda de substituție, te deconectezi desigur clasa a 7-a Algebra, în cazul în care acesta a fost utilizat pentru a rezolva sisteme de ecuatii liniare. Metoda ne amintim exemplul următor.

Exemplul 2. Pentru a rezolva sistemul de ecuații

Inmultiti toți membrii primei ecuații cu 3, iar a doua ecuație rămâne neschimbată:
Scădem a doua ecuație din prima ecuație:

Ca rezultat, adăugarea algebrică a sistemului original de două ecuații pentru a obține o ecuație mai simplă decât primul și al doilea sistem de ecuații predeterminat. Aceasta este o ecuație simplă, avem dreptul de a înlocui orice ecuație a sistemului dat, cum ar fi al doilea. Apoi, sistemul dat de ecuații este înlocuit cu un sistem mai simplu:

Acest sistem poate fi rezolvată prin substituție. Din a doua ecuație înlocuim această expresie pentru y în prima ecuație, obținem

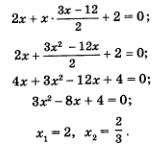
Rămâne să înlocuiască valorile găsite pentru x în formula

Astfel, am găsit două soluții:

Metoda de introducere a noilor variabile

Cu metoda de a introduce o nouă variabilă în rezolvarea ecuațiilor raționale cu o singură variabilă, întâlnim în cursul clasei a 8-algebră. Esența acestei metode pentru sistemele de ecuații de rezolvare este aceeași, dar din punct de vedere tehnic, există câteva caracteristici pe care le vom discuta în următoarele exemple.

Exemplul 3. Pentru a rezolva sistemul de ecuații

Decizie. Vom introduce o nouă variabilă Apoi, prima ecuație poate fi rescrisă într-o formă mai simplă: Să rezolve această ecuație pentru variabila t:

Ambele aceste valori satisfac condiția. și pentru că rădăcinile sunt ecuații raționale cu t variabilă. Dar apoi, orice în cazul în care, descoperim că x = 2y, sau
Astfel, metoda de introducere a unei noi variabile, am fost în stare, așa cum au fost, „stratificarea“, prima ecuație a sistemului este destul de complicată în aparență, două mai mult decât simpla ecuatie:

Ce urmează? Și apoi fiecare din cele două ecuații simple, derivate, la rândul lor au nevoie să ia în considerare sistemul ecuației x 2 - y 2 = 3, pe care nu au fost încă amintit. Cu alte cuvinte, problema se reduce la rezolvarea două ecuații simultane.

Trebuie să găsim o soluție pentru primul sistem, al doilea sistem, și toate au primit o pereche de valori pentru a include în răspunsul. Să ne rezolve primul set de ecuații:

Noi folosim metoda de substituție, mai ales pentru că aici totul este gata pentru el: 2y înlocuiască expresia x în a doua ecuație a sistemului. obținem

Deoarece x = 2y, descoperim respectiv x1 = 2, x2 = 2. Astfel preparat două soluții de sistem dat (2, 1) și (-2, -1). Noi rezolva de-al doilea set de ecuații:

Din nou, folosim metoda de substituție. 2 înlocuiască expresia y în a doua ecuație a sistemului. obținem

Această ecuație nu are rădăcini, prin urmare, sistemul de ecuații nu are nici o soluție. Astfel, răspunsul trebuie să fie pentru a include doar primele soluții de sistem.

Metoda de introducere a unor noi variabile pentru rezolvarea unui sistem de două ecuații cu două variabile utilizate în cele două variante de realizare. Prima opțiune este o nouă variabilă este introdus și utilizat într-un singur sistem de ecuații. Acesta a fost cazul în exemplu opțiunea 3.Vtoroy: două variabile noi sunt introduse și utilizate simultan în ambele ecuații ale sistemului. Deci, va fi cazul, în exemplul 4.

Exemplul 4 Pentru a rezolva sistemul de ecuații

Introducem două noi variabile:

Luați în considerare faptul că în timp ce

Acest lucru va permite să rescrie un sistem dat într-o formă mult mai simplu, dar în ceea ce privește noi variabile a și b:

Aplicăm adăugarea algebrică a unei metode de rezolvare a sistemului:

Deoarece a = 1, atunci ecuația a + 6 = 2 vom găsi: 1 + 2 = 6; 6 = 1. Astfel, variabilele a și b, avem o singură soluție:

Revenind la variabilele x și y, obținem sistemul de ecuații

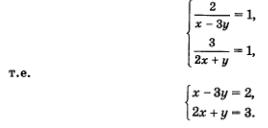
Aplicăm adăugarea algebrică a unei metode de rezolvare a sistemului:

Deoarece ecuația 2x + y = 3 găsim:
Astfel, variabilele x și y, avem o soluție:

răspundă:
Încheiem această secțiune cu o conversație teoretică destul de scurtă, dar serioasă. Ați câștigat deja o anumită experiență în relațiile cu diferite ecuații liniare:, pătrat, rațional, irațional. Știi că ideea de bază a soluției ecuației este trecerea treptată de la o ecuație la alta, mai simplu, dar este echivalent cu setul. În secțiunea anterioară am introdus conceptul de echivalență de ecuații cu două variabile. Utilizați acest concept și pentru sistemele de ecuații.

Două sisteme de ecuații cu variabile x și y sunt chemați să fie echivalente dacă au aceeași soluție, sau în cazul în care cele două sisteme nu au soluții.

Toate cele trei metode (de substituție, adiție algebrică și introducerea unor noi variabile), pe care le-am discutat în această secțiune, este absolut corect din punct de vedere al echivalenței. Cu alte cuvinte, folosind aceste tehnici, vom înlocui un sistem de ecuații de alta, mai simple, dar echivalent cu sistemul original.

Metoda grafică pentru sisteme de ecuații de rezolvare

V-am învățat să rezolve un sistem de ecuații astfel de metode comune și fiabile, cum ar fi metoda de substituție, adăugarea algebrică și introducerea de noi variabile. Și acum să ne amintim cu tine o tehnică pe care le-ați învățat deja în lecția anterioară. Asta este, să repetăm ​​ceea ce știți despre metoda grafică de soluție.

O metodă de rezolvare a sistemului de ecuații este grafic trasarea pentru fiecare dintre ecuațiile specifice sunt incluse în acest sistem și sunt în același plan de coordonate, precum și în cazul în care este necesar pentru a găsi puncte de intersecție ale acestor curbe. Pentru a rezolva acest sistem de ecuații sunt coordonatele punctului (x; y).

Trebuie reamintit faptul că sistemul de ecuații pentru grafica tind să aibă fie o soluție corectă unică, sau infinit de multe soluții sau nu au o soluție.

Acum, fiecare dintre aceste soluții mai în detaliu. Și astfel, sistemul de ecuații poate fi singura soluție, dacă directă, care sunt grafice de ecuații se intersecteaza. În cazul în care aceste linii sunt paralele, atunci sistemul de ecuații nu are absolut nici o soluție. În cazul coincidență a sistemului de ecuații mortezat directe, atunci un astfel de sistem face posibilă găsirea unui set de soluții.

Acum, să te uiți la un algoritm pentru rezolvarea unui sistem de două ecuații cu 2 necunoscute metodă grafică:

• În primul rând, în primul rând vă construi un program de prima ecuație;
• Al doilea pas este de a construi un program care aparține celei de a doua ecuație;
• În al treilea rând, trebuie să găsim punctul de intersecție a graficelor.
• Și în final vom obține coordonatele fiecărui punct de intersecție, care va fi soluția de ecuații.

Să considerăm această metodă mai în detaliu în exemplul. Ni se dă un sistem de ecuații care urmează să fie rezolvate:

1. În primul rând, vom construi un grafic al ecuației: x2 + y2 = 9.

Dar trebuie remarcat faptul că, în conformitate cu programul de ecuațiile va fi un cerc cu un centru la origine, iar raza sa este egală cu trei.

2. Următorul pas este trasarea acestei ecuații ca: y = x - 3.

În acest caz, avem de a construi o linie și pentru a găsi punctul (0, -3) și (3, 0).

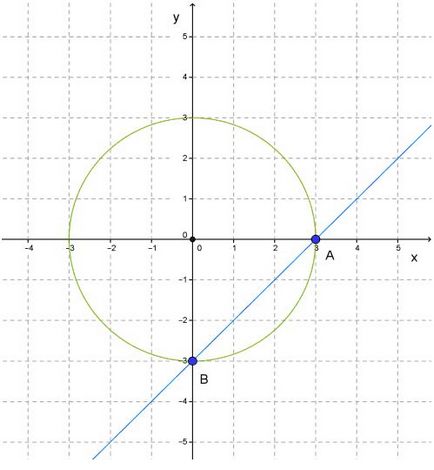
3. Să vedem ce avem. Vedem că linia intersectează cercul de la două puncte A și B.

Acum suntem în căutarea coordonatele acestor puncte. Vedem că coordonatele (3, 0) corespunde punctului A și coordonatele (0, -3), respectiv punctul B.

Și ceea ce avem ca rezultat?

Intersecția rezultantă a liniei cu cercul (3, 0) și (0, -3) sunt doar cele două soluții de ecuații. Din aceasta rezultă că numărul de date este, de asemenea, o soluție a acestui sistem de ecuații.

Aceasta este, răspunsul acestei decizii sunt: ​​(3, 0) și (0, -3).