înălțimea triunghiului, orthocenter

Distanța dintre vârful triunghiului și partea opusă se numește înălțimea. Formal, acesta este cel mai scurt interval între vârful triunghiului și (cu posibila extindere) partea opusă.

Fiecare triunghi are o înălțime de 3, care se intersectează într-un singur punct - pentru orthocenter. Dacă folosim notația standard în triunghiul ABC. Există trei înălțimi: AHa. BHB. CHC. Aceste trei segmente se intersectează într-un singur punct - (punct H în figură) orthocenter triunghiului. Pentru triunghi obtuz (având un unghi mai mare de 90 °), se află în afara orthocenter triunghiului.

Înălțimea unui triunghi acut

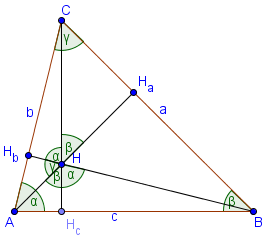
Orthocenter - un punct în interiorul unui triunghi.

∠ AHB = 180 - γ = α + β
∠ BHC = 180 - α = β + γ
∠ AHC = 180 - β = α + γ
∠ AHHc = β, ∠ BHHc = α, γ = ∠ BHHa

Înălțimea triunghi obtuz

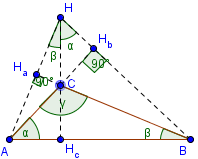
Orthocenter este în afara treugolnka.
Două înălțimi și întotdeauna se află în afara triunghiului.
∠ AHHc = ∠ CBA = β
∠ Hc HB = ∠ CAB = α

triunghi dreptunghic

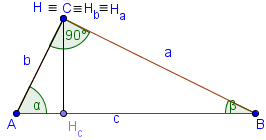
Înălțimea AHa coincide cu AC.
Acesta coincide cu înălțimea BHB BC.
Orthocenter H coincide cu C.
∠ ACHc = β, ∠ BCHc = α

R - raza circumscris
r - raza incircle
p - poluperimert: (a + b + c) / 2