funcţia pătratică

• O funcție pătratică este o funcție de forma y = ax 2 + bx + c, unde a, b, c - numere cu ≠ 0.
• Graficul unei funcții pătratică este o parabolă.

Pentru a construi graficul funcției y = x 2 un tabel de valori

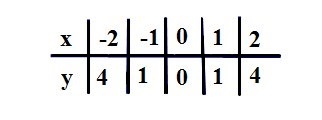
și complot folosind punctele de date:

Atenție! Dacă ecuația coeficientului pătratic o funcție de conducere = 1, atunci graficul functiei patratice are exact aceeași formă ca și graficul funcției y = x 2 pentru orice valori ale altor coeficienți.
Graful y = -x 2 are forma:

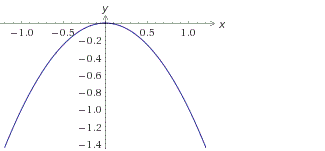
Deci:
• În cazul în care coeficientul ridicat al unui> 0, atunci ramura parabolei napravleny sus.
• Dacă cel mai mare coeficient de 2 + bx + c nevoie pentru a rezolva pătratic ecuația ax 2 + bx + c = 0.

În procesul de rezolvare a unei ecuații pătratice, descoperim discriminante: D = b 2 -4ac, care determină numărul de rădăcini ale unei ecuații pătratice.

Aici sunt trei posibilități:
1. Dacă nu există D 2 + bx + c = 0 soluții, și de aceea parabolei y = ax 2 + bx + c nu are puncte de intersecție cu axa x.
În cazul în care un> 0, graficul funcției arată astfel:

2. În cazul în care D = 0, atunci ecuația ax 2 + bx + c = 0 este o soluție, și de aceea parabolei y = ax 2 + bx + c are un singur punct de intersecție cu axa x.
În cazul în care un> 0, graficul funcției arată astfel:

3. Dacă D> 0, atunci ecuația ax 2 + bx + c = 0 are două soluții, și de aceea parabolei y = ax 2 + bx + c are două puncte de intersecție cu axa x :,
În cazul în care un> 0, graficul funcției arată astfel:

Deci, cunoscând direcția ramurilor parabolei și semnul discriminantului, putem defini în linii mari aspectul graficului funcției noastre.

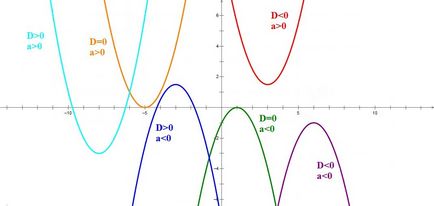
Următorul pas important în construirea graficul funcției pătratice - coordonatele varfului parabolei:

Linia prin vârful parabolei prohdyaschaya paralel cu axa OY este axa de simetrie a parabolei.

Și cu un pas plotting funcții - punctul de intersecție al parabolei y = ax 2 + bx + c pe axa OY.

Deoarece abscisa orice punct de pe axa OY este egală cu zero pentru a găsi punctul de intersecție al parabolei y = ax 2 + bx + c cu axa OY, este necesară în ecuația parabolei în loc de a substitui zero, x: y (0) = c.

Adică, punctul de intersecție cu axa parabolei OY are coordonatele (0; c).

Astfel, principalele puncte ale funcțiilor pătratice sunt grafice prezentate mai jos: