Funcția pătratică 2

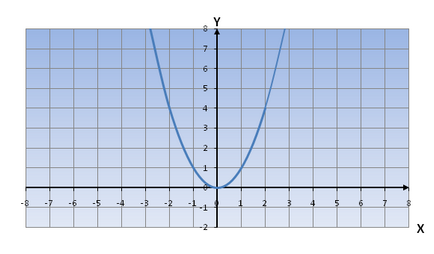
Parabolă este format din două părți: una stocată în trimestrele I unde valorile pozitive ale lui X și Y, iar a doua parte - II în sferturi, unde valori negative, X și Y sunt valori pozitive.

Dacă te duci pentru o ramură a parabolei de la -∞ la 0, observăm că funcția scade pe măsură ce se deplasează una de-a lungul cealaltă ramură a hiperbola de la 0 la + ∞, atunci vom vedea că crește funcția.

Dacă ecuația koeffitsienta senior funcție pătratică = 1, atunci graficul functiei patratice are exact aceeași formă ca și y (x) = x 2 pentru orice valori ale altor coeficienți.

Ea are forma și se bazează pe „puncte de bază“:

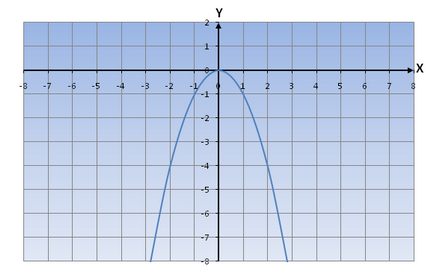
Parabolă este format din două părți: una stocată în trimestrele III, în care valorile negative, X și Y, și oa doua parte - un sfert I V unde valorile pozitive ale valorilor X și Y sunt negative.

y (x) <0, при x ∈ (-∞;0) ∪ (0;+∞)

Dacă te duci pentru o ramură a parabolei de la -∞ la 0, observăm că creșterile sa functioneze ca unul se deplasează de-a lungul cealaltă ramură a hiperbola de la 0 la + ∞, atunci vom vedea că funcția scade.

1) Domeniul funcției:

2) Domeniul de valori:

3) Cea mai mare și cea mai mică valoare a funcției:

În cazul în care un<0, то Yнаиб =0,Yнаим нет.

Dacă un> 0, toYnaim = 0, Ynaib nu.

4) Y (x) = x 2 - chiar și funcția (t.k.f (-x) = x 2 = (- x) 2 = f (x)).

Graficul este relativ simetric față de axa OY.

5) Funcțiile limitate:

Dacă un> 0, este mărginit de mai jos.

În cazul în care un<0 , функция ограничена сверху.

6) Funcția intersectează axa oX oY și punctul (0, 0)

Mutarea parabolyy (x) = x 2

Dacă adăugăm constant d (în cazul în care orice număr), ca sumand mișcării X. va avea loc de-a lungul axei parabolei (împreună cu asimptota verticală).

În acest caz, ecuația funcției va fi:

Dacă d> 0 (y (x) = (x + d) 2). graficul funcției se deplasează pe axa Ox spre stânga.

De exemplu, să considerăm ecuația y = (x + 2) 2

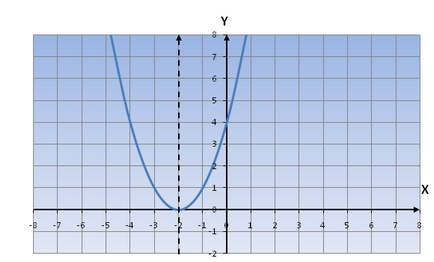
În cazul în care d<0 (y(x)=(x-d) 2 ). то график функции передвигается по оси oX вправо.

De exemplu, să considerăm ecuația y = (x-2) 2

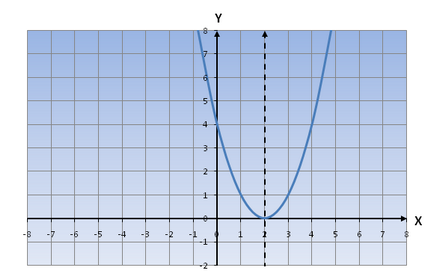
Dacă adăugăm o constanta c (c unde orice număr) la X 2 ca o completare de, va fi deplasarea axei parabolei oy (cu asimptota orizontală)

În acest caz, ecuația funcției va fi:

Dacă c> 0 (y (x) = (x) 2 + c), atunci graficul funcției pe oY se deplasează axial în sus.

De exemplu, să considerăm ecuația y = (x) 2 +2

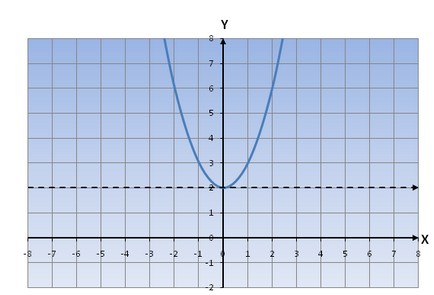
În cazul în care c <0 ( y(x)=(x) 2 -c ), то график функции передвигается по оси oY вниз.

De exemplu, să considerăm ecuația y = (x) 2 -3

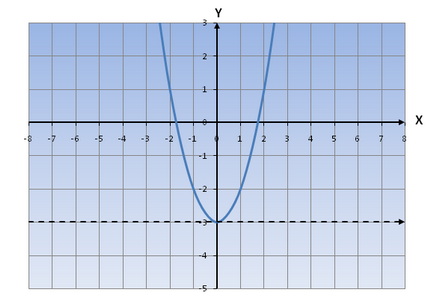
Și găsirea rădăcinile discriminante

1) 1) În cazul în care D> 0 atunci ecuația ax 2 + bx + c = 0 are două soluții, ecuația y = ax 2 + bx + c 2 are un punct de intersecție cu axa Ox:

În cazul în care un> 0, funcția grafic va avea forma aproximativă:

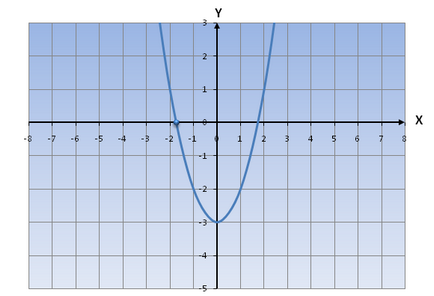
2) În cazul în care D = 0, atunci ecuația ax 2 + bx + c = 0 are o soluție de 1 => uravneniey = ax 2 + bx + c 1 este punctul de intersecție cu axa Ox.

În cazul în care un> 0, funcția grafic va avea forma aproximativă:

3) În cazul în care D<0, то уравнение ax 2 +bx+c=0 не имеет решения, => uravneniey = ax 2 + bx + c nu are puncte comune de intersecție cu axa Ox.

În cazul în care un> 0, funcția grafic va avea forma aproximativă:

Coordonatele vârful parabolei

Sunt coordonatele vârful parabolei prin aceste formule:

O linie care trece prin vârful parabolei este axa de simetrie a parabolei.

Punctul de intersecție cu osyuoY

Deoarece abscisa orice punct situată pe axa oy zero, pentru a găsi punctul de intersecție al parabolei y = ax 2 + bx + c cu axa oY, necesară în ecuația parabolei în loc Xpodstavit 0, atunci y (0) = c.

Un algoritm pentru construirea unei parabole pătratică

1) ramurile de direcție.

2) Coordonatele vârful parabolei.

3) Rădăcinile discriminante.

4) Punct suplimentar.

5) Construcția graficului.

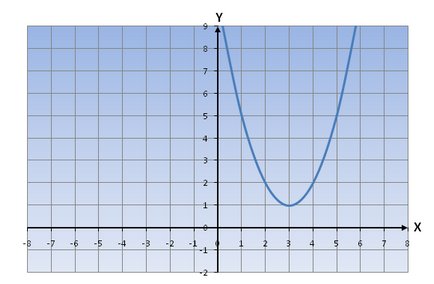
Construiți o funcție y = x 2 -6x + 15

In trinomul pătratice x 2 -6x + 15, pentru a exprima diferența pătrat folosind multiplicarea formulei Acronimul.

Formula de bază: (a ± b) = x 2 2 ± 2ab + b 2.

Ne exprimăm diferența la pătrat: x 2 -6x + 15 = (x 2 -6x + 9) +6

Punerea formula: (x 2 -6x + 9) + 6 = (x-3) 2 +6

Obținem o funcție y = (x-3) 2 +6

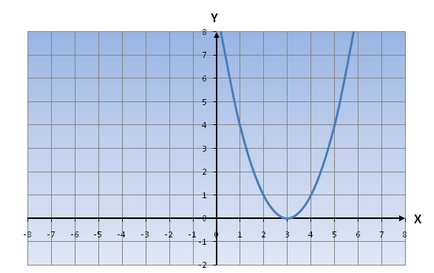
Menționăm că graficul funcției este deplasat de la 3 la axa Ox la dreapta și 6 oy axial în sus.

În consecință, graficul funcției y = (x-3) 2 6 ar arata astfel:

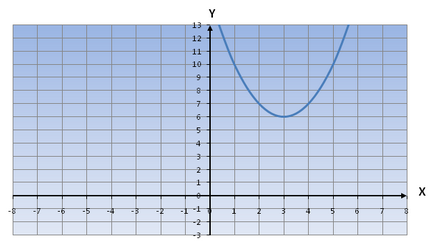
Construiți o funcție y = x 2 + 8x + 17

In trinomul pătratice x 2 + 8x + 17 pentru a exprima diferența pătrat folosind multiplicarea formulei Acronimul.

Formula de bază: (a ± b) = x 2 2 ± 2ab + b 2.

Ne exprimăm diferența la pătrat: x 2 + 8x + 17 = (x 2 + 8x + 16) +1

Punerea formula: (x 2 + 8x + 16) + 1 = (x + 4) 1 2,

Obținem o funcție y = (x + 4) 2 + 1,

Menționăm că graficul de 4 mutate la stânga și 1 oY oX axial în sus.

În consecință, graficul funcției y = (x + 4) 1 2 ar arata astfel:

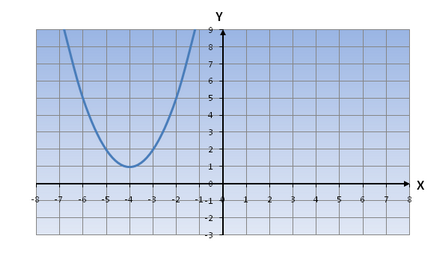
Pentru a extinde trinomul pătrat, folosind acest algoritm:

1) exprimă diferența pătrat acestei trinomial, folosind formule de multiplicare Acronim;

2) Punerea, având ca rezultat formula;

3) „citi“ graficul la un raport de compensare cu axele de coordonate;

4) construi un grafic.