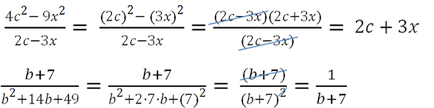fracții algebrice
La fel ca și comună fracțiunea, numărătorul (sus) și numitorul (jos) în fracțiuni algebrice.
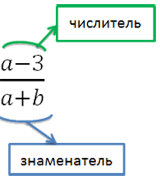
Reducerea fracțiunilor algebrice
fracții algebrice pot fi reduse. Odată cu reducerea normelor sunt reducerea fracțiilor.
Vă reamintim că în timp ce reducerea fracției comune ne-am împărtășit atât numărătorul și numitorul cu același număr.
fracții algebrice tăiat în același mod, ci doar numărătorul și numitorul sunt împărțite la același polinomul.
Luați în considerare exemplul de reducere fracții algebrice.
Determina puțin gradul în care există un monom «o». Cea mai mică rată de monom «o» este în numitor - este al doilea grad.
Se împarte atât numărătorul și numitorul prin «o 2». Atunci când împărțirea monoamele se face uz de gradul de privat.
Vă reamintim că orice literă sau un număr în gradul zero, - o unitate.
Nu este nevoie de fiecare dată pentru a înregistra detalii privind reducerea fracții algebrice. Este suficient să se aibă în vedere măsura în care a redus, și scrie doar rezultatul.
reducerea stenografie fracții algebrice după cum urmează.
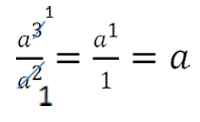
Puteți tăia doar aceleași multiplicatorilor scrisoare.
Nu poți tăia
poate fi redusă
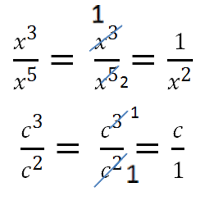
Alte exemple de reducere fracții algebrice.
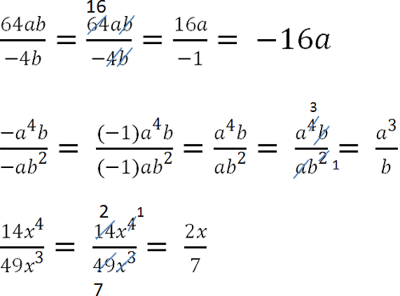
Cum de a reduce o fracție cu polinoame
Să considerăm un alt exemplu fracții algebrice. Ea vrea să reducă fracția algebrică a cărei numărător este un polinom.
Reducerea polinomială între paranteze numai cu exact același polinomul între paranteze!
În orice caz, este imposibil să taie o parte a polinomului interiorul parantezelor!
greșit
Se determină în cazul în care se termină polinomial este foarte simplu. Între polinoame poate fi doar un semn de multiplicare. Toate polinom se află în interiorul paranteze.
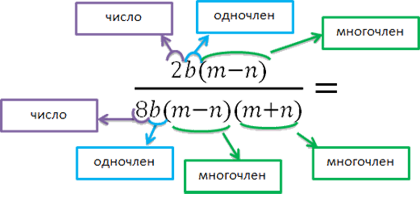
Odată ce am identificat fracția polinoamelor algebric va reduce polinomial «(m - n)» polinomială numarator cu «(m - n)» la numitor.
Exemple de reducere fracții algebrice cu polinoame.
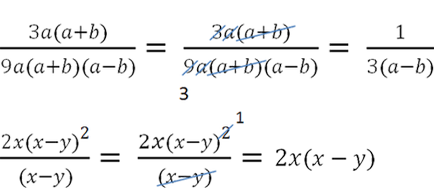
impunerea unui factor comun în reducerea fracțiilor
Pentru a fracțiilor algebrice a apărut polinoame similare, uneori, trebuie să facă un factor comun din paranteze.
reduce fracțiunile algebrice nu pot fi în această formă, deoarece polinomul
«(3f + k)» poate fi redusă numai cu polinomul «(3f + k)».
Prin urmare, pentru a obține numărătorul «(3f + k)», va prezenta un factor comun de "5".
fracțiuni Acronimul prin formule de multiplicare Acronim
In alte exemple, pentru a reduce fracții algebrice necesită
aplicând formule de multiplicare Acronim.
În forma sa inițială pentru a reduce fracția algebrică este imposibilă, deoarece nu există polinoame identice.
Dar dacă aplicăm formula pentru diferența de pătrate polinom «(a 2 - b 2)“, apar aceleași polinoame.
Alte exemple care reduc fracții algebrice utilizând multiplicarea formulelor Acronim.