Cum să demonstreze că triunghiul este ascutitunghic 1

Există experimente, al căror rezultat nu poate fi descrisă printr-un spații finite de evenimente elementare. În aceste cazuri, este uneori concept util de probabilitate geometrică.

Să presupunem că spațiul W de evenimente elementare ale unor experiment este parte a liniei reale sau a unei părți plan sau o parte a spațiului cu o măsură finită m (W). Prin pluralitate se înțelege o măsură a lungimii, suprafața și volumul respectiv. Un eveniment aleator este un spațiu submulțime W. care are finit masura m (W). Apoi, probabilitatea P (A) a evenimentului A este definit de (probabilitate geometrică).

Această metodă este folosită pentru a calcula probabilitatea când condițiile experimentale pentru probabilitatea unui eveniment elementar (punctul W a spațiului) în setul A este proporțională cu măsura prevăzută A nu depinde de localizarea în W. spațiu în acest caz, se spune că punctul aleator are o distribuție uniformă în spațiu W.

Exemplul D pe un cerc de rază plasate la întâmplare trei puncte A, B și C. Găsiți probabilitatea ca ascutitunghic triunghi ABC.

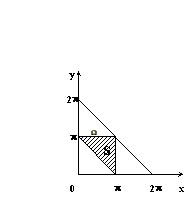
Măsurăm lungimea arcelor de cerc unitate între punctele într-o astfel de direcție încât atunci când se deplasează circumferențial dincolo de punctul A la punctul B, urmat, în conformitate cu punctul B - punctul C. Fie x - lungimea arcului AB prin y - Sun lungimea arcului. Apoi diferitele rezultate ale experimentului avute în vedere pot fi comparate în termeni HOY plane cu coordonatele x și y satisfac inegalitățile și anume.

În cazul în care evenimentul - un triunghi ABC-acută, atunci.

Evident, suprafața regiunii W este egal cu 2 p 2. și zona de S este zona. A se vedea. Fig. 1. În consecință, probabilitatea. D