Cum de a rezolva problema cu privire la funcția pătratică

Raspuns :. Zeros «y = x 2 - 3" , x1 = √ 3; x2 = - √ 3.

Cum de a găsi pentru ce valori ale «x» funcție pătratică ia valoarea numerică specificată

Pentru a găsi pentru ce valori ale «x» funcție pătratică acceptă o valoare numerică predeterminată, trebuie să:

• în loc de «y» substitut în funcție de o valoare numerică predeterminată;
• rezolvă ecuația pătratică rezultată «x».

Pentru ce valori ale lui «x» funcția «y = x 2 - x - 3" ia valoarea "-3".

Noi înlocui original funcția «y = x 2 - x - 3" , în loc de«y = -3»și de a găsi«x».

y = x 2 - x - 3

-3 = x 2 - x - 3
x 2 - x - 3 = -3
x 2 - x - 3 + 3 = 0
x 2 - x = 0
x1; 2 =

1 ± √ 1 cu 2 - 4 · 1 · 0

Răspuns: «x = 0» și «x = 1" Funcția« y = x 2 - x - 3" ia valoarea «y = -3».

Cum de a găsi coordonatele parabolei și linia de punctele de intersecție

Pentru a găsi punctul de intersecție al parabolei cu este nevoie de linia:

• echivalând partea dreaptă a funcțiilor (funcțiile acelor părți, care conțin «x»);
• rezolva ecuația rezultată pentru «x»;
• Substituind valorile numerice ale «x» în oricare dintre funcțiile, și pentru a găsi coordonatele punctelor de pe axa „Oy“.

Găsiți coordonatele punctelor de intersecție ale parabolei «y = x 2" și directă«y = 3 - 2x».

Asimilarea laturile mâna dreaptă a funcțiilor și de a rezolva ecuația rezultată pentru «x».

2 = x 3 - 2x
x 2 - 3, + 2x = 0
x 2 + 2x - 3 = 0
x1; 2 =

2 ± √ 2 2 - 4 · 1 + (-3)

Acum substituie oricare dintre funcții predeterminate (de exemplu, «y = 3 - 2x») obținut valoare numerică «x», pentru a găsi coordonatele «y» punctelor de intersecție.

1) x = 3
y = 3 - 2x
y (3) = 3 - 3 = 2 x 3 - 6 = -3
(·) A (3, 3) - primul punct de intersecție.

2) x = -1
y = 3 - 2x
y (-1) = 3 - 2 · (-1) = 3 + 2 = 5
(·) B (1; 5), - al doilea punct de intersecție.

Se înregistrează punctul de intersecție cu coordonate răspuns.

Răspuns: «y = x 2" puncte de intersecție ale unei parabole și o linie dreaptă«y = 3 - 2x»:
(·) A (3, -3) și (·) B (1; 5).

Cum se determina dacă un punct al funcției graficului parabolei aparține

Pentru a verifica dreptul de proprietate asupra punctului parabolei nu este necesară pentru a construi un grafic al funcției.

Este suficient să se substituie coordonatele punctului în formula funcției (coordonata «Ox» axa în loc de «x» și coordonatei «Oy» axa în loc de «y») și a efectua calcule aritmetice.

• Dacă aveți o adevărată egalitate, înseamnă că punctul aparține graficul funcției.
• Dacă obține paritatea greșit, punctul nu aparține funcției de program.

Nu este sistem «y = x 2" a graficului, determina care punctele îi aparțin: (+) A (2, 6). (·) B (1; 1).

Substitut în funcție «y = x 2" coordonatele punctului (+) A (2, 6).

y = x 2
6 = 02 februarie
6 = 4 (incorectă)

Deci, punctul (+) A (2, 6) nu aparține graficului «y = x 2" .

Substitut în funcție «y = x 2" coordonatele punctelor (·) B (1; 1).

y = x 2
1 = (-) 1 Feb.
1 = 1 (true)

Prin urmare, punct (·) B (-1; 1) aparține graficului «y = x 2" .

Cum de a găsi punctul de intersecție al parabolei cu axele de coordonate

Găsiți coordonatele punctelor de intersecție ale parabolei «y = x 2 -3x + 2" la axele de coordonate.

În primul rând vom defini un punct de intersecție cu funcție «Ox» axe. Pe graficul punctelor sunt după cum urmează:

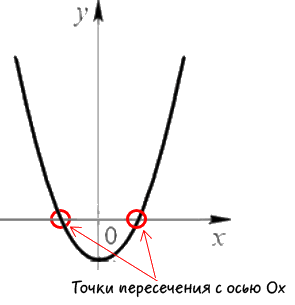
După cum se arată în figura de mai sus, coordonatele «y» la «Ox» puncte axa intersecție este zero, deci înlocuim «y = 0" în inițial funcția« y = x 2 -3x + 2" și își găsesc coordonatele «Ox» axe.

0 = x 2 -3x + 2
-3x + x 2 2 = 0
x1; 2 =

± √ 3 3 2 - 4 · 1 · 2

Scriem coordonatele generate de punctele de intersecție cu «Ox» axe: (·) A (2, 0) și (·) B (1, 0).

Acum vom găsi coordonatele punctului de intersecție cu axa Oy «».

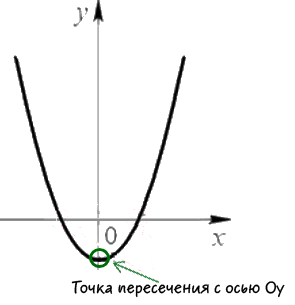
După cum se arată în figura de mai sus, coordonatele «x» intersecția cu «Oy» axa este zero.

Substituind «x = 0„în original, funcția «y = x 2 -3x + 2„și să găsească un punct de coordonate pe «Oy» axa.

y (0) = 0 2 - 3 x 0 + 2 = 2

Scrieți coordonatele unui punct obținut: (·) C (0, 2)

Scriem ca răspuns la toate coordonatele punctelor de intersecție ale axelor parabole.

Raspuns: «Ox» punct de intersecție cu axa: (·) A (2, 0) și (·) B (1, 0).
C «Oy» axe: (·) C (0, 2).

Cum se determina la ce valori de x funcției ia valori pozitive sau negative

Vă reamintim că, atunci când lucrarea spune „ia valori“ - este un valori „y“. Cu alte cuvinte, trebuie să răspundeți la întrebarea: pentru ce valori ale «x», coordonate «y» este pozitiv sau negativ.

Pentru a determina funcția a graficului, în cazul în care funcția ia valori pozitive sau negative, ar trebui să fie:

• îndeplinesc în mod direct prin punctele în locuri unde graficul traverseaza «Ox» axa;
• determină o funcție pozitivă sau negativă valoare preia intervalele dintre liniile efectuate;
• scrie răspunsul pentru fiecare perioadă de relativă «x».

Folosind graficul funcției pătratice ilustrat în Figura Răspuns: Atunci când ce valori ale «x» are funcția 1) valori pozitive; 2) valori negative.

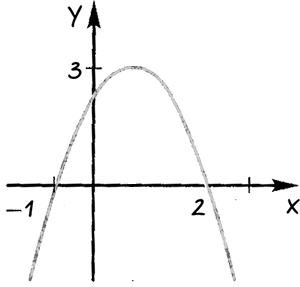
Prin punctele în care graficul funcției intersectează «Ox» axa directă.

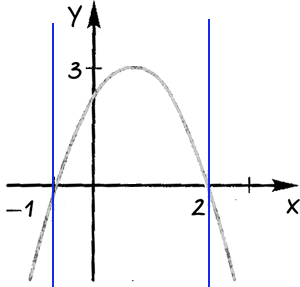
Definim regiunea în care funcția are un valori negative sau pozitive.

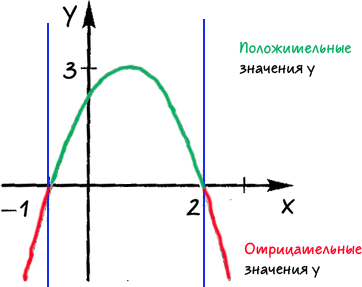
Sign peste fiecare din suprafața rezultantă, care ia valori «x» în fiecare dintre zonele selectate.

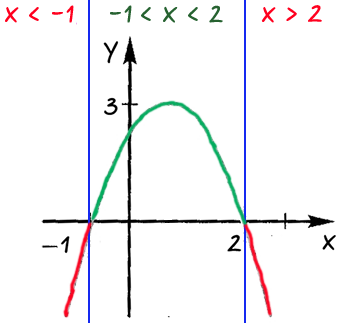
Răspuns: la «x 2" functie are o valoare negativă; când „-1