Cum de a găsi un triunghi-side

Noi spunem că aceste componente (laturi, unghiuri, etc.) determină figura în mod clar, dacă o altă figură cu aceleași componente în mod necesar egale cu originalul. De exemplu, pentru cele două laturi ale triunghiului și unghiul dintre ele, și două laterale adiacente acestuia un unghi sau trei laturi, pe baza egalității triunghiuri determinate în mod unic fiecare triunghi. Există alte cazuri, un triunghi de determinare lipsită de ambiguitate este un triunghi isoscel cu baza de date și este coborâtă în înălțime, triunghiuri la aceste trei medianele date triunghi din trei elevații etc. Este foarte important pentru rezolvarea problemei pentru a determina în mod clar figura planimetrică continuă să constate că componentele sale necunoscute, care sunt necesare pentru continuarea cursului de rezolvare a problemei.

Pentru a găsi laturile necunoscute și unghiurile unui triunghi este definit în mod unic, în general, utilizați teorema lui sinus și cosinus.
@

unde R - raza de aproximativ triunghi okruzhnosti.Teorema cosinusului

Se pare că, în determinarea unghiului triunghiului este cel mai bun pentru a găsi cosinusul decât sinusurilor. Acest lucru se datorează faptului că sinusul nu face distincție între unghiuri adiacente: cosinus distinge toate unghiurile de la 0 la p. în care unghi ascuțit pentru acesta este pozitiv pentru unghiul drept - este egal cu zero, iar unghiul obtuz - negativ, precum:.

Următorul exemplu ilustrează aplicarea sinus și cosinus teorema pentru găsirea laturile necunoscute și unghiurile unora dintre triunghiuri unice. Derulează-ți propriul.

Răspuns: a). , G = p - a - b;

b). , B = p - g - o;

@ Ca o regulă, atunci când rezolvarea triunghiuri întâi caută să definească trei părți, și apoi găsi componentele necesare. Cu cunoscute trei laturi ale triunghiului la desen mai precis imaginea miniatură trebuie să fie în măsură să determine tipul triunghiului (acută în unghi, în unghi drept sau obtuz).

Formula care rezultă din teorema cosinusului aplicată cel mai mare unghi, considerând semnul cosinusul, putem obține relația dintre laturile pătratului, permițând să se determine forma unui triunghi.

În consecință, triunghiul în care c - cea mai mare parte, este obtuz, în cazul în care; ascutitunghic dacă și dreptunghiulare când.

Exercitiul 6 .2.2.

De-a lungul lungimea celor trei laturi ale triunghiului pentru a determina tipul:

Notă. Este cunoscut faptul că în partea mai mare a triunghiului este unghiul mai mare, și invers. Cosinus unghi mai mare poate fi găsit de formula, următoarea teorema cosinusului.

Răspuns: a) și b) dreptunghiular, b) obtuz, d) ascutitunghic etc.) nu există.

În legătură cu exercitarea 6.2.2. d) trebuie remarcat destul de des aplicată în rezolvarea problemelor geometrice așa-numitul inegalitatea triunghiului. @ Trei segmente pot forma un triunghi dacă și numai dacă suma lungimilor celor mici mai lungi decât cel mai mare.

Totuși, o altă variantă de realizare, formularea este folosită inegalitatea triunghiului: Pentru orice trei puncte A, B și C au h AB - BC AC chЈ J AB + BC; în care inegalitatea din dreapta devine egalitate numai în cazul în care punctul B se află pe segmentul de curent alternativ; iar inegalitatea din stânga devine egalitate numai în cazul în care punctele A, B și C sunt coliniar și punctul B nu este conținut în segmentul de curent alternativ.

Acum vom prezenta exemple de rezolvare a unor sarcini în examenele de admitere la Universitatea de Stat Kuban.

Bazat pe AC ABC triunghi. Acesta construit ca cerc cu diametrul care intersectează laturile AB și BC în punctele M și N, respectiv. Găsiți raza cercului, dacă AB = a, și AM = a. Și CN = b. decizie

Din triunghi isoscel AOM găsi P A = (p - a) / triunghi 2. isoscel și de la CON find P C = (p - b) / 2. De aceea P B = p - P A - P C = (a + b) / 2.

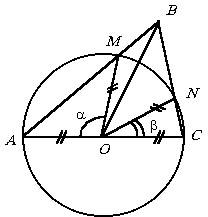
Înțeles a găsi unghiurile A și B constă în faptul că triunghiul ABC, vom cunoaște partea AB = a și două adiacente la unghiul său, și anume, D ABC este unic determinată. Rămâne de a găsi AC parte necunoscute ca în exemplul 6.2.1): și. În cazul în care raza cercului este.

Exemplul 6.2.4. (Kuban Universitatea de Stat, Math. 1979)

În triunghiul ABC cerc înscris. Puncte D, E, F - punct de tangență laturi AB, BC, CA, respectiv. Se determină suprafața triunghiului ABC. dacă AB = a, BC = b, R DEF = 60 °.

Această referință este interesant în acest raționament D ABC conform de mai jos va fi determinată în mod unic. Cu toate acestea, cu astfel de componente nu pot fi nu mai mult de două triunghiuri diferite! decizie

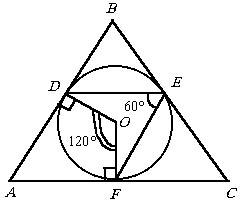
Să O - centrul cercului inscris. Deoarece DEF unghiul inscris este de 60 °. DOF unghiul central este de 120 °. Suma unghiurilor în ADOF patrulater egală cu 360 °. Deci, noi știm despre triunghiul ABC, cele două părți AB = a, BC = b. și unghiul A (nu între ele!).

În continuare, ne străduim să găsim o terță parte de curent alternativ. Presupunând că AC = x, avem cosinus și Teorema. Locație. Apoi vom găsi zona triunghiului ABC formula.
Răspunsul este ambiguu!

Notă. Este recomandabil să nu se limitează la răspunsul în rezolvarea problemei anterioare.

Deci, în cazul în care, (de exemplu), problema nu are nici o soluție.

În cazul în care aceeași sau b> a. (Ie, fie), atunci problema are o soluție unică :.

A fost doar atunci când (care) am arătat anterior o întoarcere de două cifre.

Acum, pentru aplicarea triunghiului ilustrațiilor inegalității prezintă soluția unei simple examene orale de sarcini la Facultatea de matematică de la Universitatea de Stat Kuban.

Dovedește că suma celor două medianele unui triunghi este mai mică decât perimetrul său. evidență

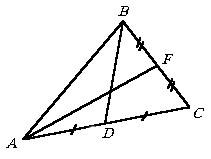
Prin inegalitatea triunghiului D ABF și D ACF au AF

În cazul în care, în mod analog din D ABD și D CBD. 2 BD obține <, а значит 2AF + 2 BD <2 и AF + BD <. что и требовалось доказать.

Demonstrati ca orice triunghi ABC D. orice punct care se află în interiorul acestuia sau pe o parte, lungimea segmentului este mai mică decât AD semiperimetrul triunghiului ABC.

Notă: Utilizați argumente similare cu cele date la începutul dovada lucrarea anterioară.

Pentru a încheia această secțiune vom prezenta trei sarcini tipice, soluție din care rolul principal jucat de teorema lui cosinus.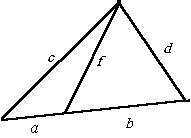

Pentru a ilustra a decide a).

a) Având în vedere: a, b, c, d. Găsiți f.

b) Având în vedere: a, b, c, f. Găsiți d.

c) Având în vedere: a, c, d, f. Găsiți b.

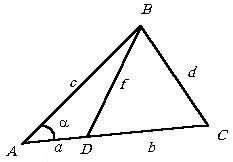
Prezentăm P în continuare A = a. De la D ABC descoperire
.
Apoi, de la D ABD găsi.
și anume .

Sarcini b) și c) să decidă pe cont propriu. Rețineți că în soluția b), ca într-o), poate fi doar o singură valoare pentru segmentul de lungime necunoscută, iar lucrarea în) două posibile valori dorite pentru b.

FORWARD | Înapoi | PRIMA PAGINA | planimetrie | stereometrie