Cum de a crea o matrice de 1

Determinarea matricei și a elementelor sale. Desemnări.

Matrix - un tabel cu $ m $ rândurile și $ n $ coloane. Elementele matricei pot fi de natură destul de diversă de obiecte: numere, variabile, sau, de exemplu, alte matrice. De exemplu, matricea $ \ stânga (\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta) $ cuprinde 3 rânduri și 2 coloane; elementele sale sunt numere întregi. Matricea $ \ left (\ începe o a ^ 2 + 9 9 \ Sin x \\ -9 3t ^ 2-4 u-t 8 \ end \ dreapta) $ cuprinde 2 rânduri și 4 coloane.

Diferite moduri de matrici de înregistrare: spectacol \ ascunde

Matricea poate fi scrisă nu numai în runda, dar între paranteze drepte sau linii duble. Ie a declarat înregistrarea înseamnă sub aceeași matrice:

$$ \ stânga (\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta); \; \; \ Stânga [\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta]; \; \; \ Stânga \ Vert \ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta \ Vert $$

Produsul de $ m \ ori n $ este numit dimensiunea matricei. De exemplu, în cazul în care matricea conține 5 linii și 3 coloane, se vorbește de o dimensiune matrice de 5 $ \ $ 3 ori. Matricea $ \ stânga (\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta) $ este de $ \ cu 3 ori 2 $.

De obicei, matricea sunt notate cu literele alfabetului latin: $ A $, $ B $, $ C $ și așa mai departe. De exemplu, $ B = \ stânga (\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta) $. Linia de numerotare merge de sus în jos; coloane - de la stânga la dreapta. De exemplu, primul rând al matricei $ B $ conține elemente 5 și 3, iar a doua coloană conține elementele 3, -87, 0.

elemente de matrice sunt de obicei notate cu litere mici. De exemplu, elementele matricei sunt notate $ A $ $ a_ $. Indicele dual $ $ ij conține informații despre poziția elementului în matrice. Numărul $ i $ - este numărul liniei, iar numărul $ j $ - numărul coloanei, care se află la intersecția unui element de $ a_ $. De exemplu, la intersecția din al doilea rând și coloana a cincea din matricea $ A = \ left (\ begin 51 37 -9 0 9 97 \\ 1 2 3 41 59 6 \\ -17 -15 -13 -11 -8 -5 \\ 52 31 -4 -1 17 90 \ end \ dreapta) $ este un element de $ a_ = $ 59:

In mod similar, la intersecția primului rând și element de prima coloană au $ a_ = $ 51; la intersecția treilea rând și coloana a doua - element de $ a _ = - $ 15 și așa mai departe. Rețineți că înregistrarea $ a_ $ citit ca „doi și trei“, dar nu „un treizeci-doi.“

Pentru prescurtare matrice notația $ A $, a cărei mărime este egală cu $ m \ ori n $, folosit de înregistrare $ A_ $. Acesta poate fi scris și desfășurat alte câteva:

în care înregistrarea $ (a _) $ denumire înseamnă elementele de matrice $ A $. În extins complet matriceal $ A _ = (a _) $ poate fi scrisă ca:

$$ A _ = \ left (\ începe a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \ end \ dreapta) $$

Introducem un alt termen - matrice egal.

Două matrici de dimensiuni egale $ A _ = (a _) $ și B _ = $ (b _) $ a spus să fie egale. dacă elementele respective sunt egale, adică, $ A_ = B_ $ pentru toate $ i = \ overline $ și $ j = \ overline $.

Înregistrarea "$ i = \ overline $" indică faptul că parametrul $ i $ variază de la 1 la m. De exemplu, salvând $ i = \ overline $ indică faptul că parametrul $ i $ ia valorile 1, 2, 3, 4, 5.

Deci, pentru egalitatea matricilor necesară îndeplinirea a două condiții: mărimea unui meci și egalitatea elementelor corespunzătoare. De exemplu, matricea $ A = \ stânga (\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta) $ nu este egal cu matricea $ B = \ stânga (\ începe 8 -9 \\ 0 -87 \ end \ dreapta) $, deoarece matricea $ A $ este $ 3 \ ori $ 2, iar dimensiunea matricei este de $ B $ 2 $ \ ori $ sau 2. De asemenea, matrice $ O matrice $ nu este egal cu $ C = \ stânga (\ începe 5 3 \\ 98 -87 \\ 8 0 \ end \ dreapta) $, deoarece $ a_ \ neq C_ $ (de exemplu, $ 0 \ neq $ 98). Dar, pentru $ matricea F = \ left (\ începe 5 3 \\ 0 -87 \\ 8 0 \ end \ dreapta) $ se poate scrie în siguranță $ A = F $ ca și dimensiuni, precum și elementele corespunzătoare ale matricelor $ A $ și $ F $ coincid.

Se determină mărimea $ matricea A = \ left (\ începe -1 -2 1 \\ 5 9 -8 -6 \\ 8 23 \\ 11 -12 -5 \\ 4 0 -10 \\ \ end \ dreapta) $. Indicați care sunt elementele $ a_ $, $ a_ $, $ a_ $.

Această matrice conține 5 rânduri și 3 coloane, astfel încât dimensiunea de 5 $ \ ori ei 3 $. Pentru această matrice, puteți utiliza, de asemenea, numele $ $ A_.

$ A_ $ Element situat la intersecția a primului rând și coloana a doua, cu toate acestea $ a _ = - $ sau 2. Element $ a_ $ situat la intersecția al treilea rând și coloana a treia, astfel încât $ a_ = $. 23 element de $ $ A_ situat la intersecția al patrulea rând și coloana a treia, deci $ a _ = - $ 5.

Tipuri de matrici în funcție de mărimea lor. Principal și secundar diagonală. Trasarea unei matrice.

Să presupunem că o anumită matrice $ A_ $. Dacă $ m = 1 $ (matricea constă dintr-o singură linie), matricea predeterminată este un șir de matrice. Dacă $ n = 1 $ (matrice este format dintr-o singură coloană), apoi o matrice se numește matrice coloană. De exemplu, $ \ left (\ începe -1 -2 0 -9 8 \ end \ dreapta) $ - matrice rând și $ \ left (\ begin -1 \\ \\ 5 6 \ end \ dreapta) $ - matricea coloană.

Dacă matricea $ A_ $ true condiție $ m \ neq n $ (adică, numărul de linii nu este egal cu numărul de coloane), se spune adesea că $ A $ - matrice dreptunghiulară. De exemplu, matricea $ \ left (\ începe -1 -2 0 9 \\ 5 9 5 1 \ end \ dreapta) $ este $ 2 \ ori $ 4, adică Acesta cuprinde 2 rânduri și 4 coloane. Deoarece numărul de linii nu este egal cu numărul de coloane, această matrice este dreptunghiular.

Dacă matricea $ A_ $ true condiție $ m = n $ (adică, numărul de rânduri este egal cu numărul de coloane), atunci spunem că $ A $ - matrice pătratică de ordinul $ n $. De exemplu, $ \ left (\ începe -1 -2 \\ 5 9 \ end \ dreapta) $ - matrice pătrată de ordinul al doilea; $ \ Stânga (\ începe -1 -2 9 \\ 5 9 8 \\ 1 0 4 \ end \ dreapta) $ - matricea pătrată a treia comanda. În general, pătrat matrice $ A_ $ poate fi scris ca:

$$ A _ = \ left (\ începe a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \ end \ dreapta) $$

Ei spun că elementele $ a_ $, $ a_ $, $ \ ldots $, $ a_ $ situat pe diagonala principală a matricei $ A_ $. Aceste elemente sunt numite elementele diagonale principale (sau elemente pur și simplu diagonale). Elements $ a_ $, $ a_ $, $ \ ldots $, $ a_ $ situat pe latura (secundar) diagonală; acestea sunt numite elemente laterale-diagonală. De exemplu, pentru $ matricea C = \ stânga (\ begin2-291 \\ 598 0 \\ 1 0 4 -4 -7 \\ -9 5 6 \ end \ dreapta) $ avem:

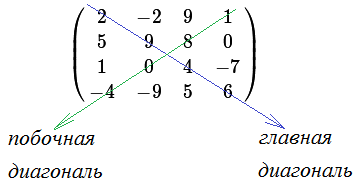
Elements $ C_ = 2 $, $ C_ = 9 $, $ C_ = 4 $, $ C_ = 6 $ sunt principalele elemente diagonale; elemente $ C_ = 1 $, $ C_ = 8 $, $ C_ = 0 $, $ c _ = - $ 4 - elemente diagonale laterale.

Suma principalelor elemente diagonale se numește Trasarea matricei și este notat cu $ \ Tr A $ (sau $ \ Sp A $):

De exemplu, pentru matricea $ C = \ stânga (\ 2 începe -2 9 1 \\ 5 9 8 0 \\ 1 0 4 -7 \\ - 4 -9 5 6 \ end \ dreapta) $ avem:

Conceptul elementelor diagonale este de asemenea utilizat pentru matrici non-pătrate. De exemplu, pentru $ matricea B = \ stânga (\ 2 începe -2 9 1 7 \\ 5 -9 8 0 -6 \\ 1 0 4 -7 -6 \ end \ dreapta) $ principalele elemente diagonale sunt $ B_ = 2 $, $ b _ = - 9 $, $ B_ = $, 4.

Tipuri de matrici în funcție de valoarea elementelor lor.

Dacă toate elementele matricei $ A_ $ egală cu zero, atunci această matrice se numește zero și este de obicei notat cu litera $ O $. De exemplu, $ \ left (\ 0 începe 0 \\ 0 0 \\ 0 0 \ end \ dreapta) $, $ \ left (\ 0 începe 0 0 \\ 0 0 0 \\ 0 0 0 \ end \ dreapta) $ - de la zero matrici.

Să matrice $ $ A_ este după cum urmează:

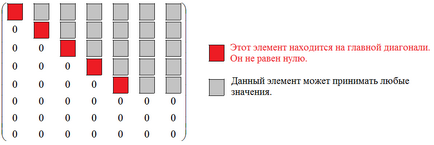
Apoi, această matrice se numește trapez. Este posibil să nu conțină nici rânduri, dar în cazul în care acestea sunt, sunt situate în partea de jos a matricei. Mai general matrice trapezoidal poate fi scrisă ca:

Din nou, nu este necesară prezența zero linii la sfârșitul anului. Ie este tehnic posibil să se aloce astfel de condiții pentru matrice trapezoidal:

1. Toate elementele situate sub diagonala principală sunt egale cu zero.
2. Toate elementele $ a_ $ la $ a_ $, situată pe diagonala principală, nu sunt egale cu zero: $ a_ \ neq 0 \; a_ \ neq 0, \ ldots, a_ \ neq 0 $.
3. Fie toate elementele anterioare $ m-r $ rânduri egale cu zero sau $ m = r $ (adică la zero rânduri nu sunt prezente la toate).

Exemple trapezoidale matrici:

Ne întoarcem la următoarea definiție. $ Matrix $ A_ numit viteză. în cazul în care îndeplinește următoarele condiții:

1. Primul element al primului rând este nenulă, $ a_ \ neq 0 $.
2. Fiecare șir nenul (adică un șir care conține cel puțin un element nu este egal cu zero) este compusă din două părți: prima (zero) și o a doua porțiune care pornește de la elementul nenul:

Dintre cele două rânduri nenule, care sunt de mai jos, în care zero este de multe ori mai mult.

line Nul pot fi aranjate doar după rândurile nenuli.

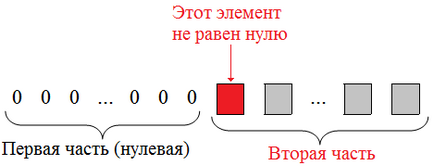
De exemplu, matricea pas va fi:

Pentru comparație, matricea $ \ left (\ 2 începe -2 0 1 \\ 0 0 8 7 \\ 0 0 4 -7 \\ 0 0 0 0 \ end \ dreapta) $ nu este un pas, pentru că al treilea rând de zero este aceeași ca și în al doilea rând. Ie Acesta încalcă principiul „linia de jos - cea mai mare parte de la zero.“ Ar trebui să adaug că matricea trapezoidală este un caz special al unei matrice în trepte.

Ne întoarcem la următoarea definiție. Dacă toate elementele unei matrice pătratică dispus sub diagonala principală sunt egale cu zero, atunci această matrice se numește matrice superior triunghiulară. De exemplu, $ \ left (\ 2 începe -2 9 1 \\ 0 9 8 0 \\ 0 0 4 -7 \\ 0 0 0 6 \ end \ dreapta) $ - matrice triunghiulară superioară. Rețineți că definiția matricei triunghiulară superioară nu spune nimic despre valorile elementelor situate deasupra diagonalei principale, sau pe diagonala principală. Acestea pot fi nul sau nu - acest lucru nu este esențial. De exemplu, $ \ left (\ 0 începe 0 9 \\ 0 0 0 \\ 0 0 0 \ end \ dreapta) $ - de asemenea, o matrice triunghiulară superioară.

Dacă toate elementele unei matrice pătratică dispus deasupra diagonalei principale sunt egale cu zero, atunci această matrice se numește matrice triunghiulară inferior. De exemplu, $ \ left (\ begin 3 0 0 0 \\ -5 1 0 0 \\ 8 2 1 \\ 0 5 4 0 6 \ end \ dreapta) $ - matrice triunghiular inferior. De notat că definiția unei matrice triunghiulare inferior nu se spune nimic despre valorile elementelor dispuse la sau pe diagonala principală. Acestea pot fi nul sau nu - nu contează. De exemplu, $ \ left (\ începe -5 0 0 \\ 0 0 0 \\ 0 0 9 \ end \ dreapta) $ și $ \ stânga (\ începe 0 0 0 \\ 0 0 0 \\ 0 0 0 \ end \ dreapta) $ - matrici triunghiulare, de asemenea, mai mici.

O matrice pătrată se numește diagonală. în cazul în care toate elementele acestei matrice care nu se află pe diagonala principală sunt zero. Exemplu: $ \ left (\ begin 3 0 0 0 \\ 0 -2 0 0 \\ 0 0 0 0 \\ 0 0 0 6 \ end \ dreapta) $. pe principalele elemente diagonale pot fi orice (zero sau nu) - acest lucru nu este esențial.

O matrice diagonală se numește o unitate. dacă toate elementele acestei matrice, situate pe diagonala principală sunt egale cu 1. De exemplu, $ \ stânga (\ începe 1 0 0 0 \\ 0 1 0 0 \\ 0 0 1 0 \\ 0 0 0 1 \ end \ dreapta) $ - matricea de identitate a patra ordine; $ \ Stânga (\ începe 1 0 \\ 0 1 \ end \ dreapta) $ - matricea identitate de ordinul al doilea.