Cosinus și sinus cum să rezolve
Pentru a rezolva inegalitățile trigonometrice simple. . . (În loc de eticheta poate fi ..) sunt utilizate, mod grafic. Găsiți punctul de intersecție al graficului cu linia funcțională corespunzătoare. situate mai aproape de origine, și apoi utilizate periodicitatea funcției.
Pentru mai multe inegalități trigonometrice complexe a redus la cazul lor cea mai simplă prin intermediul simplificării.
Grafice și proprietățile de bază ale funcțiilor trigonometrice.
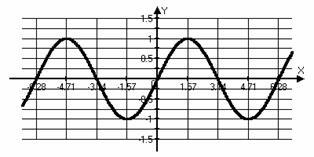
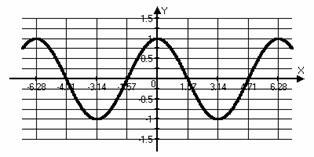
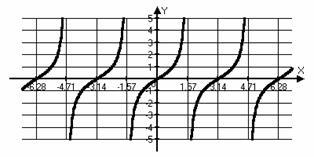
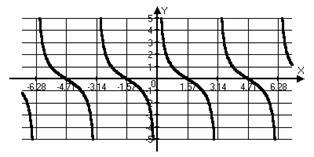
Grafice și proprietățile de bază ale funcțiilor trigonometrice inverse.
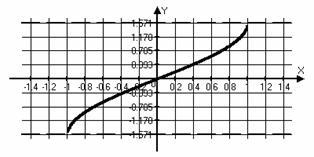
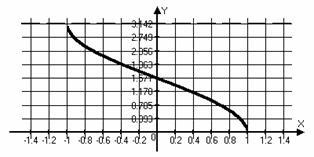
Funcția sau chiar sau impar
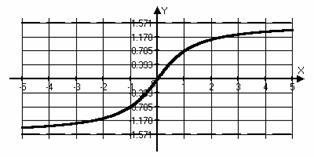
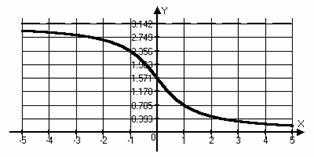
Funcția sau chiar sau impar
Funcții de comunicare trigonometrice inverse funcțiilor trigonometrice efectuate de către următorul tabel
Astfel, valoarea expresiei 0.
Explicație Secțiunea: Soluție de ecuații trigonometrice și inegalități.
Pentru a rezolva ecuații trigonometrice arbitrare și inegalități aplică aceleași tehnici de bază care au fost descrise anterior pentru solutia de ecuatii algebrice: introducerea unei noi variabile și factoring partea stângă a unei ecuații sau inegalități.
Din considerațiile generale, precizează următoarele: înlocuirea unei funcții altele pentru a evita introducerea de radicali, deoarece complică soluția și necesită verificarea rădăcinilor găsite (în construcția ecuației puterii poate să apară rădăcini străine).
Uneori este posibil, transferul toți termenii în partea stângă a ecuației, sa răspândit asupra factorilor.
1. Ecuații și relativ omogene.
Fiecare din ecuațiile:
și este omogenă în ceea ce privește. Suma exponenților y și toți membrii aceleiași ecuații. Această sumă se numește gradul ecuației omogene. Împărțind de. gradul ecuației omogene, aceasta poate fi redusă la o ecuație în ceea ce privește algebric.
Despartitor, de exemplu, pe ecuația. obținem ecuația:
Atunci când aceste ecuații sunt echivalente, ca și în cazul în care. apoi prima ecuație obținem asta. că este imposibil (și același argument nu dispar). Apoi, din ecuația echivalentă găsim. rezolvarea unei ecuații pătratice. și pe valorile - valorile corespunzătoare.
4. Rezolva ecuația:
Decizie. Și înlocuirea. Obținem ecuația omogenă:
Vom introduce o nouă variabilă, și obținem o ecuație pătratică pentru ea:
Rădăcinile acestei ecuații. În continuare, vom obține un set echivalent de ecuații:
2. Ecuațiile, dintre care stânga este descompus în factori, iar partea dreaptă este zero.
Transferarea tuturor termenilor orice ecuație din partea stângă, poate fi redus la forma.
În cazul în care partea stângă a acestei ecuații este descompus în factori, fiecare dintre ele este egal cu zero, iar ecuația descompune în câteva ecuații simple. Este important să se țină seama de faptul că rădăcinile ecuației inițiale sunt numai cele din rădăcini de ecuații obținute care se încadrează în domeniul ecuației inițiale.
5. Rezolva ecuația:
Decizie. Aici, este recomandabil să se utilizeze formulele de transformare a funcțiilor trigonometrice funcționează în valoare. Folosind aceste formule, obținem ecuația:
Cosinusul diferenței transformă într-un produs. care este echivalent cu setul de ecuații:
Aceste ecuații pot fi soluționate printr-o substituție trigonometrice universal. folosind formule și exprimarea prin.
Ecuația inițială este redusă la o ecuație algebrică rațională, soluția pe care am discutat anterior.
Aceste ecuații sunt rezolvate prin introducerea unghi auxiliar mai rațional :. Luați în considerare cursul ulterior rezolvarea ecuației prin intermediul unor transformări echivalente laterale din stânga:
Rețineți că expresia în paranteze, în acest caz, convertit la o cosinusul diferenței dintre argumentele:
Astfel, ecuația originală este echivalentă cu ecuația trigonometrice simplu:
soluția care, sunt
Problema este rezolvată într-o formă generală.
6. Rezolva ecuația:
Vom introduce o nouă variabilă: și de a obține o ecuație pătratică echivalentă.
în care discriminante este zero și, prin urmare, au o singură rădăcină. Problema se reduce la rezolvarea ecuației:
Decizie. (A doua metodă). Noi introducem unghiul auxiliar :.
Apoi, soluția ecuației inițiale o dată scrisă sub forma:
Cu alte cuvinte, am primit același răspuns, ceea ce nu este surprinzător.