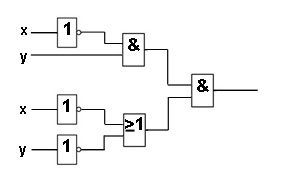
circuite logice și tabele de adevăr
circuite logice trebuie să fie implementate în dispozitive digitale funcții booleene (funcții booleene).
În circuitele digitale a unui semnal digital - un semnal care poate lua două valori, considerate ca fiind o logică „1“ și „0“ logic.
circuite logice sunt puse în aplicare pe elementele logice, „NU“, „SI“, „SAU“, „ȘI-NU“, „NOR“, „XOR“ și „echivalență“. Primele trei elemente logice vă permit să pună în aplicare orice funcție logică în mod arbitrar complexe în baze Boolean. Vom rezolva problema pe logica aceasta pusă în aplicare într-o bază boolean.
Pentru a indica elementele logice folosind mai multe standarde. Cele mai frecvente sunt americane (ANSI), european (DIN), International (IEC) și Română (GOST). Următoarea figură prezintă denumirile de elemente logice în standarde (pentru imagine mai mare pot face clic pe butonul din stânga al mouse-ului).
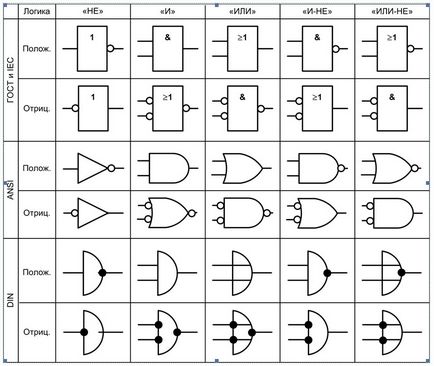
În această lecție, vom rezolva problema pe logica pe care elementele logice sunt desemnate de către standardul GOST.
Analiza logica sarcinii
Sarcina analiză este de a determina functia f. a implementat o logică prestabilită. În rezolvarea acestei probleme, este convenabil să urmeze următoarea secvență de acțiuni.
- Circuitul logic este împărțit în niveluri. Rangurilor sunt atribuite numere consecutive.
- Ieșirea fiecărui element logic este numele funcției dorite, echipat cu indicele digitale, în cazul în care prima cifră - număr de nivel și cifre rămase - numărul de ordine al elementului din categoria.
- Pentru fiecare element este scris expresie analitică care leagă funcția de ieșire a variabilelor de intrare. Expresia este determinată de funcția logică implementată în conformitate cu elementul logic.
- Schimbare se realizează unele funcții de ieșire prin intermediul celuilalt, până când nu au o funcție booleană, exprimată în termeni de variabilele de intrare.
Exemplul 1: Găsiți o logică funcție booleană și de a face un tabel de adevăr pentru circuitul logic.
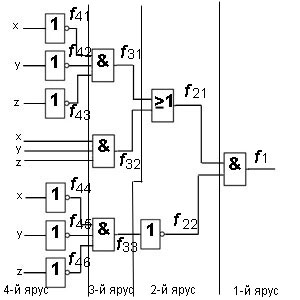
Decizie. Împărțiți logica pe ranguri care au arătat deja. Scriem toate funcțiile, pornind de la nivel 1 st:
Acum scrie toate funcțiile prin înlocuirea variabilei de intrare x. y. z:
Ca rezultat, obținem o funcție care implementează logica de ieșire:
Tabelul de adevăr pentru această schemă logică:
Exemplul 3. Găsiți logica funcția boolean și de a face un tabel de adevăr pentru circuitul logic.
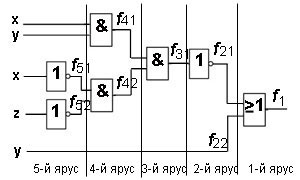
Decizie. Schema logică Divizarea niveluri. Structura acestei logici, spre deosebire de exemplele anterioare, are 5 nivele în loc de variabila 4. Dar o intrare - cele mai mici - trece prin toate nivelurile și direct intră poarta în primul nivel. Scriem toate funcțiile, pornind de la nivel 1 st:
Acum scrie toate funcțiile prin înlocuirea variabilei de intrare x. y. z:
Ca rezultat, obținem o funcție care implementează logica de ieșire:
Tabelul de adevăr pentru această schemă logică:
Sinteza în logica sarcinii
Proiectarea logică pentru descrierea analitică a schemei este problema de logica nume de sinteză.
Fiecare disjuncție (suma logică) corespunde elementului „OR“, numărul de intrări este determinat de numărul de variabile din disjuncției. Fiecare conjuncției (produs logic) corespunde elementului „și“ numărul de intrări este determinat de numărul de variabile în conjuncție. corespunde „NO“ Fiecare element de negare (inversiune).
Dezvoltarea logicii de multe ori începe cu o definiție a funcției logice, care trebuie să pună în aplicare logica. În acest caz, numai având în vedere logica tabelul de adevăr. Ne vom uita la doar un astfel de exemplu, că este, vom rezolva problema pe dos logica a discutat mai sus sarcină de analiză.
Exemplul 4. Construirea unui circuit logic care implementează funcția cu dată tabelul de adevăr:
Decizie. Parse tabela de adevăr pentru circuitul logic. Definim o funcție care este obținută la ieșirea circuitului intermediar și funcțiile de intrare poate avea argumente x și y. Prima linie a rezultatului punerii în aplicare a funcției de ieșire la acea valoare a variabilelor de intrare sunt egale cu una, să fie o logică „0“, în al doilea rând - pentru diferite valori ale variabilelor de intrare pe ieșire trebuie să fie, de asemenea, o logică „0“. Prin urmare, este necesar ca funcția de ieșire a fost o conjuncție (produs logic).
Acum selectați funcțiile intermediare. Obținem următorul tabel pentru funcțiile intermediare și funcțiile de ieșire - conjuncția funcții intermediare:
Pentru a construi logica necesare elemente care implementează operațiile logice indicate în funcția de ieșire, plasate în ordinea dată de această funcție. De exprimare, care au nevoie de 3 „NU“, schema, circuitul cu două intrări „și“ și o schemă cu două intrări „SAU“. În conformitate cu funcția de ieșire obținem următoarea logică: