Cele mai simple de ordinul unu ecuații diferențiale, exemple, solutii

In acest articol vom face cu soluția dintre cele mai simple de prim ordin ecuații diferențiale care nu conțin funcția necunoscută y. Aceste ecuații diferențiale sunt fie deja rezolvate pentru derivatul, sau pot fi rezolvate în ceea ce privește derivatul.

Soluția generală a ecuațiilor diferențiale ale formei la un interval predeterminat X poate fi găsit prin integrarea de ambele părți ale acestei ecuații. Obținem. Dacă ne întoarcem la proprietățile integralei nedeterminată. apoi ajunge la dorit soluție totală y = F (x) + C unde F (x) - una din funcția primitivelor f (x) în intervalul X. și C - este o constantă arbitrară.

Rețineți că intervalul de X nu este indicat în mai multe probleme. În acest caz, aceasta înseamnă că soluția trebuie căutată pentru toate x. și în care funcția necunoscută y. și ecuația originală au sens.

Dacă doriți să găsiți o soluție particulară a ecuației diferențiale care satisface condiția inițială y (x0) = y0. după constatarea integralei totală y = F (x) + C. încă mai trebuie să se calculeze valoarea constanta C = C0. Folosind starea inițială. Aceasta este, constanta C = C0 se determină din ecuația F (x0) + C = y0. și ecuația diferențială particulară dorită este de forma y = F (x) + C0. Să considerăm un exemplu.

Găsiți soluția generală a ecuației diferențiale, verifică corectitudinea rezultatului. Găsiți o soluție specială a acestei ecuații care îndeplinește condiția inițială.

Integrarea ecuației diferențiale inițiale, obținem. Aceasta integrantă ia metoda de integrare de către părți:

Astfel, - soluția generală a ecuației diferențiale.

Pentru a verifica acuratețea rezultatului controlului. La această soluție rezultată să substituie ecuația originală:

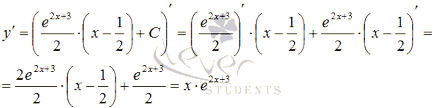
Prin urmare, atunci când ecuația inițială devine o identitate, astfel încât soluția generală a ecuației diferențiale a constatat în mod corect.

Trebuie remarcat faptul că soluția găsită este soluția generală a ecuației diferențiale pentru toate valorile valide ale argumentului x.

Rămâne să se determine soluția particulară a ode cu condiția inițială. Cu alte cuvinte, aveți nevoie pentru a găsi o valoare de constante C la care va fi adevărată egalitate.

Prin urmare, substituind C = 2 în soluția generală a TAC se obține o soluție particulară a unei ecuații diferențiale care satisface o condiție inițială predeterminată.

ecuație diferențială ordinară poate fi rezolvată pentru derivatul, împărțind ambele părți cu f (x). O astfel de transformare ar fi echivalent dacă f (x) nu este egal cu zero, sub orice x în intervalul de integrare a ecuației diferențiale X.

Pot exista cazuri când ambele rândul său, la zero, pentru anumite valori ale argumentului x ∈ X functia f (x) și g (x). Pentru astfel de valori ale lui x soluția generală a ecuației diferențiale este orice funcție de y. le-a definit ca.

Dacă argumentul pentru unele x ∈ X valori ale condițiilor, atunci odă nu are soluții.

Pentru intervalul x repaus X soluție generală a ecuației diferențiale se determină din ecuația convertită. Să luăm în considerare următoarele exemple.

Găsiți soluția generală a ecuației diferențiale ordinare.

Pentru că știm proprietățile de bază ale funcțiilor elementare care funcția logaritm natural definite pentru valori pozitive ale argumentului, oricât de domeniu al funcției y = ln (x + 3) este intervalul x> -3. În consecință, ecuația diferențială inițială are o semnificație pentru x> -3. La aceste valori ale expresiei argument x + 3 nu devine nulă, prin urmare, poate fi rezolvată pentru derivatul TAC, împărțind ambele părți cu x + 3 devine.

Acum trebuie să se integreze ecuațiile diferențiale care rezultă rezolvate pentru derivatul :. Pentru a lua acest integrantă folosim metoda de a asocia un semn al diferențial. . Astfel, - soluția generală a ecuației diferențiale pentru x> -3.

Găsiți toate soluțiile ecuației diferențiale.

Ecuația diferențială are sens pentru orice x reală. Dacă presupunem că x ≠ 0. acesta poate fi transformat în forma de ODE. Când x = 0 ecuația de pornire devine o identitate pentru funcțiile definite la x = 0. Astfel, atunci când x = 0 soluție a ecuației diferențiale este orice funcție de y. determinat la argumentul zero.

Noi integra ecuația diferențială:

- ecuație diferențială, atunci când x = 0 soluție a ecuației diferențiale este orice funcție definită pentru această valoare a argumentului.

Găsiți soluția generală a ecuației diferențiale ordinare.

sinx dispare pentru. Pentru aceste argumente COSX ≠ 0. Prin urmare, valoarea la ecuația diferențială inițială nu are nici o soluție. În acest caz, putem împărți ambele părți de sinx. Obținem oda rezolvat pentru derivatul. Integrați-l :. Astfel, - soluția generală a unei ecuații diferențiale.

• Èl'sgol'ts LE ecuații diferențiale și calculul variațiilor.