Zăcând în cruce unghiuri de linii paralele sunt egale

Există o teorema care liniile sunt paralele, dacă la intersecția secțiunii transversale situată în cruce unghiuri sunt egale. Având în vedere aici - unghiuri egale la cruce stau tăiere, un rezultat - liniile sunt paralele.

Există o teoremă inversă situată unghiurile în cruce intersectate sunt egale atunci când traversează linii paralele. În acest caz, este dat - linii paralele, rezultat - egalitate situată în cruce, care se intersectează în unghiuri.

Este teorema conversa „excesivă“? Nu pot să spun doar că singurele linii paralele situate unghiuri în cruce, care se intersectează sunt egale? Dar poate fi, aceste unghiuri sunt egale, iar unele nu sunt în linii paralele. Aceasta este, în paralel, în mod clar sunt, dar există și alte linii, de asemenea, cu unghiuri egale. Teorema conversa exclude o astfel de posibilitate.

Dovada inversa Teorema reduce la următoarele.

Se presupune contrariul, adică. E. Că liniile de date paralele situate unghiuri în cruce intersectate nu sunt egale. Să presupunem că liniile paralele a și b, care traversează transversal c. Să presupunem că culcate cruce unghiurile 1 și 2 nu sunt egale: ∠1 ≠ ∠2.

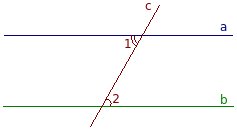
După punctul de intersecție secantă cu una dintre liniile paralele (b) trage o linie dreaptă d, astfel încât să se obțină unghi egal colț situată transversal 1 3: ∠1 = ∠3.

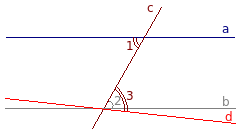
Teorema directă prevede că, atunci când unghiurile situate în cruce, care se intersectează sunt egale, atunci liniile sunt paralele. Prin urmare, liniile A și D sunt paralele: a || d.

Se dovedește că un punct comun (care se suprapun liniile drepte b, c, d) a efectuat două linii paralele (b Ĺ? I d), care sunt paralele cu linia a. Cu toate acestea, de la o teoremă a dovedit anterior, acest lucru nu poate fi: printr-un punct care nu se află pe o linie dreaptă, puteți desena doar o singură linie paralelă.

Prin urmare, presupunând că ∠1 ≠ ∠2, nu este adevărat. De aceea ∠1 = ∠2. Nu există nici o altă linie dreaptă care trece printr-un punct dat, ceea ce ar da unghiuri egale, la secțiunea transversală, cu excepția numai paralele.