Volumul unei prisme
Care este volumul prismei și cum să-l găsiți
Volumul Prism - este produsul din suprafața bazei sale și înălțimea.
Cu toate acestea, știm că baza prismei poate fi un triunghi, un pătrat sau orice alt poliedru.
Prin urmare, pentru a găsi volumul de prisme, trebuie doar pentru a calcula aria bazei prismei, și apoi această zonă înmulțită cu înălțimea sa.
Aceasta este, în cazul în care baza prismei triunghi, trebuie mai întâi să găsească mijloacele în zona de triunghi. Dacă baza prismei este un pătrat sau un alt poligon, trebuie mai întâi să se uite zona de pătrat, sau alt poligon înseamnă.
Rețineți că înălțimea prismei este perpendicular, atras la baza prismei.
Ce este o prismă
Și acum să ne amintim definiția unei prisme.
Prism - un poligon, cele două fețe (baze) din care se află în planuri paralele, și toate muchiile sunt paralele cu exteriorul acestor fețe.
Pur și simplu pune, ea:
Prism - este orice formă geometrică care are două baze egale între ele și plate fețe.
Titlul prismei depinde de forma sa de bază. Când baza este o prismă triunghi, astfel încât un apel prismă triunghiulară. prisme multiple fațete se numește o figură geometrică, a cărui bază este un poliedru. De asemenea, prismă - un fel de cilindru.
Ce tipuri de prisme sunt
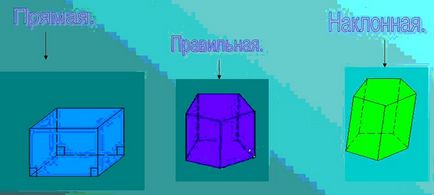
Dacă ne uităm la imaginea de mai sus, vedem că prismele sunt drepte, drept și oblic.
1. Ceea ce se numește prisma corectă?
2. De ce se numește asta?
3. Care este numele unei prisme ale cărei baze sunt poligoane regulate?
4. Care este înălțimea figurii?
5. Cum se numește o prismă, ale cărei margini nu sunt perpendiculare?
6. Dă definiția unei prisme triunghiulare.
7. Poate fi paralelipipedică prismă?
8. Care este figura geometrică numit un poligon semiregulate?
Care sunt elementele este o prismă
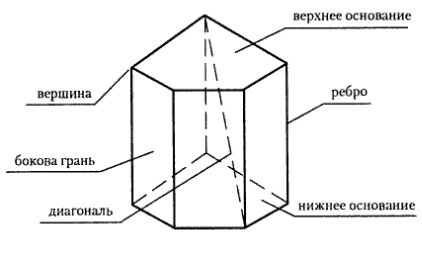
Prisma este format din elemente de bază, cum ar fi inferioară și superioară, fețele laterale, muchii și vârfuri.
• Ambele bazei prismei și se află în planuri paralele între ele.
• fețele laterale ale piramidei - este un paralelogram.
• Suprafața laterală a piramidei este suma fețelor laterale.
• fețele laterale laterale comune, nu este nimic altceva decât marginile laterale ale figurii.
• Înălțimea piramidei este un segment de legătură pentru planul de masă și perpendicular pe acesta.
proprietăţi prismă
Cifra geometrică, ca o prisma, are un număr de proprietăți. Să aruncăm o privire mai atentă la aceste proprietăți:
• În primul rând, bazele prismei sunt numite poligoane regulate;
• În al doilea rând, la fețele laterale ale prismei sunt prezentate sub forma unui paralelogram;
• În al treilea rând, această formă geometrică nervurile sunt paralele și egale;
• În al patrulea rând, suprafața totală a prismei este:
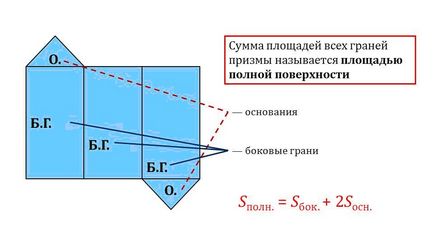
Acum, ia în considerare teorema care oferă o formulă cu care suprafața laterală calculată a demonstrației.

fapte interesante despre prisma
V-ați gândit vreodată de un astfel de fapt interesant că prisma poate fi nu numai un corp geometric, dar, de asemenea, alte obiecte din jurul nostru. Chiar și fulg de nea obișnuită în funcție de temperatura se poate transforma în prismă de gheață, luând forma de forme hexagonale.
Dar cristale de calcit au un astfel de fenomen unic ca să se dezintegreze în fragmente și să ia cutia forma. Și cel mai surprinzător, pe ceea ce ar fi piese de mici, nu sunt zdrobite cristale de calcit, rezultatul este întotdeauna același, se transforma intr-o cutie tiddly.
Se pare că o prismă a câștigat popularitate nu numai în matematică, demonstrând corpul său geometric, dar, de asemenea, în arte, pentru că ea este baza de picturi create de mari artiști precum Picasso, Braque, Griess și altele.