Sinus, cosinus, tangentă și cotangentă în trigonometrie

În acest articol, vom arăta modul de a furniza definiții ale sinus, cosinus, tangentă și cotangentă unghiului și numărul în trigonometrie. Aici vorbim despre notația, vom da exemple de înregistrări care dau o ilustrare grafică. În cele din urmă vom trage o paralelă între definițiile sinus, cosinus, tangentă și cotangentă în geometrie și trigonometrie.

Navigare în pagină.

Definiția sinus, cosinus, tangentă și cotangentă

Un unghi ascuțit într-un triunghi dreptunghic

De cunoscut, desigur geometrie determinarea sinus, cosinus, tangentă și cotangentă unghi ascuțit într-un triunghi dreptunghic. Ele sunt date ca un raport de laturile unui triunghi dreptunghic. Aici sunt declarațiile lor.

Sinusul unui unghi ascuțit într-un triunghi dreptunghic - este raportul dintre piciorul opus ipotenuzei.

Cotangentă unui unghi ascuțit într-un triunghi dreptunghic - raportul dintre partea adiacentă unui opus.

Există, de asemenea, să introducă sine notație, cosinus, tangentă și cotangentă - păcat. cos. și tg respectiv ctg.

De exemplu, dacă ABC - triunghi înclinat cu unghiul drept C. sinusul unghiului acut este egal cu raportul dintre piciorul opus ipotenuzei BC AB. adică, sin∠A = BC / AB.

Aceste definiții fac posibilă calcularea valorilor sinus, cosinus, tangentă și cotangentă un unghi ascuțit de cunoscute lungimile laterale triunghi și valorile cunoscute ale sinus, cosinus, tangenta, cotangentă și lungimea uneia dintre părți pentru a găsi lungimea celelalte laturi. De exemplu, dacă știm că cateta AC dreptunghiular triunghi și ipotenuza este egal cu 3. 7. AB este egal cu am putea calcula cosinusul unghiului ascuțit A, prin definiție: cos∠A = AC / AB = 3/7.

unghi de rotație

În trigonometria un unghi începe să arate mai pe larg - să introducă conceptul de unghiul de rotație. Mărimea unghiului de rotație, opus unui unghi ascuțit nu este limitat la domeniul de la 0 la 90 de grade, unghiul de rotație în grade (în radiani) pot fi exprimate în orice număr real dorit din -∞ la + ∞.

În această lumină, având în vedere definiția sinus, cosinus, tangentă și cotangentă nu este un unghi ascuțit, iar unghiul de orice magnitudine - unghi de rotație. Acestea sunt date prin coordonatele x și y punctul A1. în care așa-numitul punctul A inițial (1, 0), după rotirea acestuia printr-un unghi α în jurul punctul O - care pornește cartezian rectangular sistem și centrul cercului unitate de coordonate.

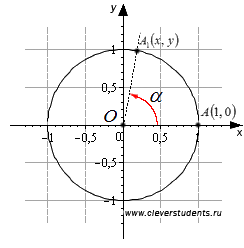
Sinusul unghiului de rotație α - este ordonata punctului A1. adică, sinα = y.

Cotangentă unghiului de rotație α este raportul dintre punctul A1 abscisă la ordonata acesteia, adică ctgα = x / y.

Sinus și cosinus sunt determinate pentru fiecare unghi α. deoarece putem determina întotdeauna abscisa și ordonata punctului, care se obține prin rotirea punctului inițial la un unghi α. O tangentă și cotangentă nu sunt definite pentru orice unghi. Tangent nu determină pentru alfa aceste unghiuri. în care punctul de plecare se mută la punctul cu abscisa de la zero (0, 1) sau (0, -1). iar acest lucru are loc la unghiuri de 90 ° + 180 ° · k. k∈Z (π / 2 + π · k rad). Într-adevăr, la aceste unghiuri de exprimare rotație tgα = y / x este lipsit de sens, deoarece are o divizie de zero. În ceea ce privește cotangentă, acesta nu este definit pentru alfa asemenea unghiuri. în care punctul de plecare se mută la un punct cu zero, ordonata (1, 0) sau (-1, 0). așa cum este cazul cu unghiuri de 180 ° · k. k∈Z (π · k rad).

Astfel, funcțiile sinus și cosinus sunt definite pentru toate unghiurile de rotație, tangent definită pentru toate unghiurile cu excepția 90 ° + 180 ° · k. k∈Z (π / 2 + π · k rad) și cotangentă - pentru toate unghiurile cu excepția 180 ° · k. k∈Z (π · k rad).

Definițiile apar deja cunoscute pentru a ne referi la păcat. cos. și tg CTG. acestea sunt utilizate pentru a desemna sinus, cosinus, tangenta și unghiul de rotație cotangentă (uneori să fie găsit notație de culoare cafenie și pat de copii. tangenta responsabil și cotangentă). Deoarece sinusul unghiului de rotație de 30 de grade poate fi scris ca sin30 °. înregistrări tg (-24 ° 17 „) și tangent ctgα întâlni unghiul de rotație -24 grade 17 minute și cotangentă unghiului de rotație α. Să ne amintim că simbolul unghiului „rad“ este adesea omis măsură radiani în timpul înregistrării. De exemplu, cosinusul unghiului de rotație în trei pi rad notat de obicei COS3 · π.

Pentru a încheia această secțiune este de remarcat faptul că într-o conversație despre sine, cosinus, tangenta și cotangentă a unghiului de rotație este adesea omis expresia „rândul său colțul“ sau cuvântul „rotație“. Adică, în loc de expresia „unghi alfa sinusoidală de rotație“ este de obicei folosit expresia „sinusul unghiului alfa“ sau chiar mai scurt - „sinus alfa“. Același lucru este valabil și pentru cosinusul și tangenta și cotangentă.

De asemenea, să spunem că definițiile sinus, cosinus, tangentă și cotangentă unghi ascuțit într-un triunghi dreptunghic sunt în concordanță cu definițiile date doar sinus, cosinus, tangentă și unghiul cotangentă valorii de rotație de la 0 la 90 de grade. Acest lucru se explică în ultimul paragraf al acestui articol.

În continuare există o nevoie pentru a scăpa de colțuri și să dea definiția sinus, cosinus, tangentă și numărul cotangentă mai degrabă decât unghiul.

Sinus, cosinus, tangenta, cotangentă și t este numărul de egal sinus, cosinus, tangentă și cotangentă unghiului de rotație în radiani t respectiv.

De exemplu, cosinusul 8 · π prin definiție este un număr egal cu cosinusul unghiului 8 · π rad. Un cosinusul unghiului 8 · π rad este egal cu unitatea, astfel încât cosinusul 8 · π este egal cu 1.

Există o altă abordare pentru a determina numărul sinus, cosinus, tangentă și cotangentă. Constă în faptul că fiecare număr real t îi este atribuit un punct de pe cercul unitate centrat la dreptunghiular sistem de coordonate, și sinus, cosinus, tangenta, cotangentă și definit prin coordonatele acestui punct. Să examinăm acest lucru mai detaliat.

Vom arăta cum să setați corespondența dintre numerele reale și punctele de cerc:

• de la 0 este atribuit un punct de pornire A (1, 0);
• număr pozitiv T este atribuit un punct de pe cercul unitate, pe care o vom primi, dacă ne mișcăm într-un cerc din punctul de pornire într-o direcție invers acelor de ceasornic și du-te prin lungimea căii t;
• negativ întreg T este atribuit un punct de pe cercul unitate, pe care o vom primi, dacă ne mișcăm într-un cerc din punctul de plecare în sensul acelor de ceasornic și du-te prin lungimea căii | t |.

Acum vom merge la definițiile sinus, cosinus, tangenta și cotangentă t. Să presupunem că numărul t corespunzător A1 punctul cercului (x, y) (de exemplu, numărul pi / 2; A1 corespunde punctului (0, 1)).

Sinus numitul număr punct t ordonata cercului unitate care corespunde numărului t. adică, = y sint.

Cosinus punctului t abscisa numit cercul unitate care corespunde numărului t. adică, costul = x.

t Tangent este raportul dintre ordonata la abscisa punctului de cercul unitate care corespunde numărului t. adică, TGT = y / x. O altă formulare echivalentă a tangenta t - este raportul dintre sinusul la cosinusul acestui număr, adică, sqltype = sint / costuri.

Cotangentă de abscisa este raportul dintre t este dată de ordonata cercul unitate care corespunde numărului t. adică ctgt = x / y. O altă formulare este după cum urmează: tangenta t - este raportul dintre t cosinus la sinusul t. ctgt = cost / sint.

Aici observăm că doar definiția de date este în concordanță cu definiția dată de la începutul acestui paragraf. Într-adevăr, punctul de pe cercul unitate care corespunde numărului t. Acesta coincide cu punctul care rezultă din punctul de început de rotație cu un unghi în radiani t.

O alta este de a clarifica acest punct. Să presupunem că avem un sin3 record. De unde știi despre sinusului de 3 sau unghiul de rotație al sinusului 3 radiani în cauză? De obicei, este clar din context, altfel nu are, probabil, nici o valoare de bază.

Funcții trigonometrice de argument unghiular și numeric

Conform definițiilor din paragraful anterior, fiecare unghi de rotație α corespunde unei valori certă a sinα. ca valoarea cos. Mai mult decât atât, toate rotația diferite unghiuri de 90 ° + 180 ° · k. k∈Z (π / 2 + π · k rad) corespund tg valorilor. dar diferit de la 180 ° · k. k∈Z (π · k rad) - valori ctgα. Prin urmare, sinα. cosα. și tgα ctgα - este o funcție de unghiul a. Cu alte cuvinte - este o funcție de argumentul unghiular.

În mod similar, putem vorbi despre funcțiile sinus, cosinus, tangenta și cotangentă argumentului număr. De fapt, fiecare număr t reală corespunde unei certă valoare Sint. precum și a costurilor. În plus, toate celelalte decât π / 2 + π · k numere. k∈Z corespund valorilor TGT. iar numărul tt · k. k∈Z - valori ctgt.

Funcțiile sinus, cosinus, tangentă și cotangentă numit funcțiile trigonometrice de bază.

Din context, este clar, de obicei, cu functii trigonometrice de argumente unghiulare sau un argument numeric care ne ocupăm. În caz contrar, putem presupune că variabila independentă ca o măsură a unghiului (argument unghiular) și un argument numeric.

Cu toate acestea, școala este studiat în principal funcții numerice, de exemplu, funcții ale căror argumente ca valorile corespunzătoare ale funcției sunt numerele. Prin urmare, dacă vorbim despre funcții, este recomandabil să se ia în considerare funcțiile trigonometrice funcționează argumente numerice.

definiții de comunicare ale geometriei și trigonometria

Dacă luăm în considerare unghiul α valoare de la 0 la 90 de grade, apoi datele în contextul trigonometrie determinarea sinus, cosinus, tangenta și cotangentă unghiului de rotație sunt în deplină concordanță cu definițiile sinus, cosinus, tangentă și cotangentă unghi ascuțit într-un triunghi dreptunghic, care sunt în curs de geometrie. Să-l dovedesc.

Zugrăvi într-un sistem de coordonate cartezian rectangular Oxy unitate cerc. Observați punctul de pornire A (1, 0). Rotiți-l printr-un unghi α valoare de la 0 la 90 de grade, vom obține punctul A1 (x, y). Picătură de la punctul A1 pe axa Ox perpendiculare A1 H.

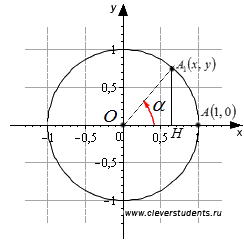
Este ușor de observat că în triunghi unghiul A1 OH egal cu unghiul de rotație α. Lungimea adiacente acestui colț al piciorului OH egal cu punctul abscisă A1. adică | OH | = x. lungimea piciorului opus cu unghiul A1 H A1 este egal cu punctul ordonatei. adică | A1 H | = y. OA1 și lungimea ipotenuzei este egal cu unu, deoarece este o rază unitate de cerc. Apoi, prin definirea geometriei unghiului sinusoidale acute într-un subunitatea triunghi dreptunghic este egal cu A1 OH opuse relație cu piciorul ipotenuza, adică sinα = | A1 H | / | OA1 | = y / y = 1. Și prin definirea sinus trigonometrică a unghiului de rotație a este egală cu ordonata punctului A1. adică, sinα = y. Acest lucru arată că determinarea unghiului ascuțit sinusoidale în triunghi echivalent în unghi drept pentru determinarea sinusul unghiului de rotație α cu α de la 0 la 90 de grade.

In mod similar, se poate arăta că determinarea cosinus, tangenta și cotangentă unghi ascuțit α în concordanță cu unghiul definițiilor cosinus, tangentă și cotangentă de rotație α.