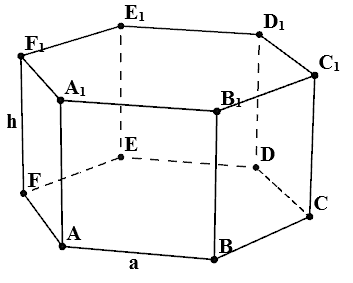
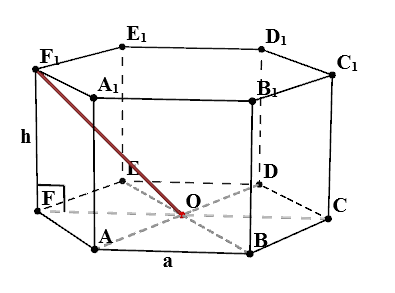
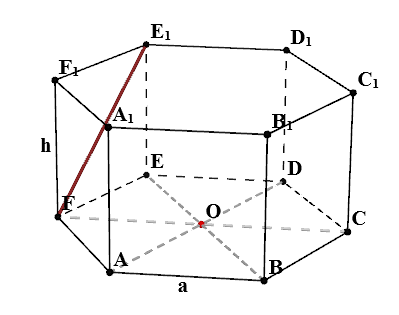
prismă regulată hexagonală - o prismă a cărui bază se află două hexagon regulat, și toate fețele laterale în mod substanțial perpendicular pe aceste motive.
denumiri
- $ ABCDEFA_1B_1C_1D_1E_1F_1 $ - prismă hexagonală regulată
- $ A $ - lungime laterală a bazei prismei
- $ H $ - lungimea marginii laterale a prismei
- $ S _> $ - baza de prismă pătrată
- $ S _> $ - zona din partea laterală a prismei
- $ S _> $ - suprafața totală a prismei
- $ V _> $ - suma de Prism
Suprafața bazei prismei
Bazele prismei sunt hexagoane regulate cu laturile $ a $. Conform proprietăților unui hexagon regulat, baze prismatice pătrat este $$ S _> = \ frac> \ cdot a ^ 2 $$ Astfel, se pare că $ s_ = S _ = \ frac> \ cdot o ^ 2 $.
Suprafața totală a prismei
Suprafața totală a prismei este format din zone ale fețelor laterale ale prismei și suprafața de bază. Fiecare dintre fețele laterale ale prismei este un dreptunghi cu laturile $ a $ și $ h $. Prin urmare, proprietățile dreptunghiului $$ S _> = o \ cdot h $$ Y prism șase fețe laterale și două baze, de aceea, aria suprafeței sale totale este $$ S _> = 6 \ cdot S _> + 2 \ cdot S _> = 6 \ cdot un \ cdot h + 2 \ cdot \ frac> \ cdot a ^ 2 $$
Volumul unei prisme
Volumul prismei este calculat ca produs al zonei bazei sale la înălțimea sa. Înălțimea prismei regulată este una din marginile sale laterale, cum ar fi de margine $ AA_1 $. La baza prismă hexagonală regulată este un hexagon regulat, o zonă cunoscută pentru noi. Obținem $$ V _> = S _> \ cdot AA_1 = \ frac> \ cdot a ^ 2 \ cdot h $$
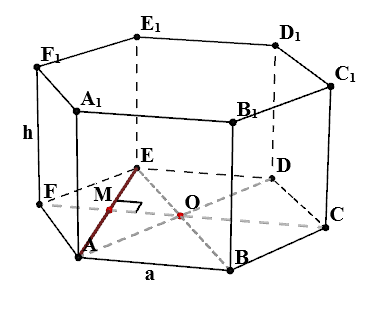
hexagon regulat în baza prismei
Considerăm un ABCDEF hexagon regulat, care se află la baza prismei. Cheltuim segmentele AD, BE și CF. Lăsați intersecția acestor segmente este punctul O. Conform proprietăților unui hexagon regulat, triunghiuri AOB, BOC, COD, DOE, EOF, FOA sunt triunghiuri drepte. Rezultă că $$ AO = OD = EO = OB = CO = = unui fir $$ tăiat AE, se intersectează cu CF segment la isoscel M. AEO Triangle, există $ AO = OE = a, \ \ unghiul EOA = $ la 120 ^. Conform proprietăților unui triunghi isoscel $$ AE = a \ cdot \ sqrt = \ sqrt \ cdot un $$ În mod similar, putem concluziona că $ AC = CE = \ sqrt \ cdot un $, $ FM = MO = \ frac \ cdot un $.
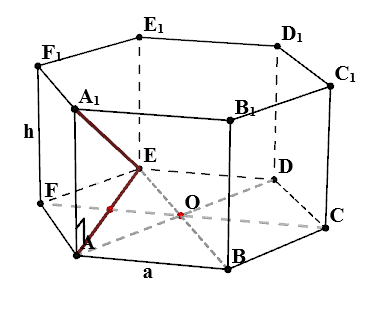
Găsiți $ EA_1 $
În triunghiul $ AEA_1 $:
- $ AA_1 = h $
- $ AE = \ sqrt \ cdot un $ - așa cum am tocmai am aflat
- $ \ Unghi EAA_1 = 90 ^ $ - proprietăți de prismă regulată
Astfel, se pare că triunghiul $ AEA_1 $ dreptunghiulară. Conform proprietăților unui triunghi dreptunghic $$ EA_1 = \ sqrt = \ sqrt $$ Dacă $ h = un $, apoi $$ EA_1 = 2 \ cdot o $$ Ca urmare argumente similare obținem că $ FB_1 = AC_1 = BD_1 = CE_1 = DF_1 = \ sqrt $.
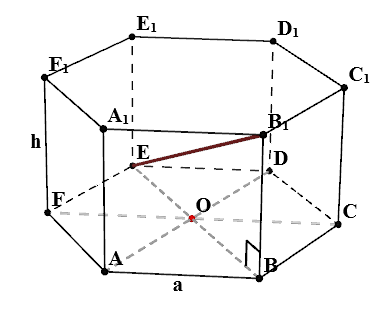
Am găsit $ EB_1 $
În triunghiul $ BEB_1 $:
- $ BB_1 = h $
- $ BE = 2 \ cdot un $ - pentru că $ EO = OB = un $
- $ \ Unghi EBB_1 = 90 ^ $ - proprietăți de prismă regulată
Astfel, se pare că triunghiul $ BEB_1 $ dreptunghiulară. Conform proprietăților unui triunghi dreptunghic $$ EB_1 = \ sqrt = \ sqrt $$ Dacă $ h = un $, apoi $$ EB_1 = \ sqrt \ cdot un $$ este obținut după un argument similar care $ FC_1 = Ad_1 = BE_1 = CF_1 = DA_1 = \ sqrt $.
Găsiți $ OF_1 $
În triunghiul $ FOF_1 $:
- $ FF_1 = h $
- $ FO = a $
- $ \ Unghi OFF_1 = 90 ^ $ - proprietăți de prismă regulată
Astfel, se pare că triunghiul $ FOF_1 $ dreptunghiulară. Conform proprietăților unui triunghi dreptunghic $$ OF_1 = \ sqrt = \ sqrt $$ Dacă $ h = un $, apoi $$ OF_1 = \ sqrt \ cdot un $$ este obținut după un argument similar care $ OA_1 = OB_1 = OC_1 = OD_1 = OE_1 = \ sqrt $.
Găsiți $ FE_1 $
În triunghiul $ FEE_1 $:
- $ EE_1 = h $
- $ FE = a $
- $ \ Unghi FEE_1 = 90 ^ $ - proprietăți de prismă regulată
Astfel, se pare că triunghiul $ FEE_1 $ dreptunghiulară. Conform proprietăților unui triunghi dreptunghic $$ FE_1 = \ sqrt = \ sqrt $$ Dacă $ h = un $, apoi $$ FE_1 = \ sqrt \ cdot o $$ Ca urmare argumente similare constatăm că lungimea diagonalelor celelalte fețe laterale ale prismei sunt de asemenea egale cu $ \ sqrt $.