Planificarea optimă 1

Problema, la care acum ne întoarcem la discuție, se numește planificarea optimă. Facilități de planificare poate fi foarte diferit de sistem: activitățile individuale de întreprindere, industrie sau agricultură, din regiune, în cele din urmă, a statului. Declarația problemei planificării este după cum urmează:

• Există unele ținte: x, y, și altele;

• Există unele resurse: R1 R2 și alții, datorită cărora aceste obiective pot fi atinse. Aceste resurse sunt aproape întotdeauna limitate;

• există un anumit obiectiv strategic, care depinde de valorile lui x, y, și alte obiective, care ar trebui să fie orientate de planificare.

Este necesar să se determine valoarea obiectivelor ținând cont de resursele limitate, sub rezerva realizării obiectivelor strategice. Acest lucru va fi cel mai bun plan.

Iată câteva exemple. Lăsați obiectul de planificare este gradinita. Noi ne limităm la cele două cifre țintă: numărul de copii și numărul de cadre didactice. Principalele resurse ale activității grădinițelor sunt mărimea finanțării, și suprafața podelei. Care sunt obiectivele strategice?

Desigur, una dintre ele este păstrarea și întărirea sănătății copiilor. O măsură cantitativă a acestui obiectiv este acela de a reduce la minimum incidența elevilor de grădiniță.

Un alt exemplu: planificarea activităților economice ale statului. Desigur, este prea dificil o sarcină pentru noi să-l înțelegem pe deplin. Ținte foarte mult: este volumul de producție de diferite tipuri de producție industrială și agricolă, planul de formare, cantitatea de energie electrică generată, mărimea salariilor angajaților din sectorul public, și mai mult. Resursele includ :. Numărul populației în vârstă de muncă, bugetul de stat, resursele naturale, energia, posibilitatea de a sistemelor de transport, etc. După cum vă puteți imagina, fiecare dintre aceste tipuri de resurse este limitat. În plus, cea mai importantă resursă este timpul alocat pentru punerea în aplicare a planului. Problema obiectivelor strategice destul de complicate. Statul are o mulțime de ei, dar în diferite perioade ale istoriei prioritățile obiectivelor pot varia.

Dacă vrem să utilizați un computer pentru a rezolva problema de planificare optimă, avem nevoie din nou pentru a construi un model matematic. Prin urmare, tot ceea ce a fost spus la începutul acestei secțiuni, trebuie să fie traduse în limba de numere, formule, ecuații, și alte mijloace de matematică. În întregime, această sarcină este foarte dificil pentru sistemele reale. Ca și înainte, vom lua calea simplificării.

Să considerăm un exemplu foarte simplu, de la care obține o idee de o abordare pentru rezolvarea problemei planificării optime.

Exemplu. Scoala cofetăria pregătește plăcinte și prăjituri. Datorită capacității de stocare limitată pe zi, puteți găti în acest fel nu cumulează mai mult de 700 de produse. zi de lucru în magazinul de patiserie durează 8 ore. Dacă problema numai prăjituri, ziua se poate face nu mai mult de 250 de bucăți de plăcinte puteți face 1000 în cazul în care nu produce prăjituri. Costul turtei este de două ori mai mare decât Patty. Este necesar pentru a face un plan de producție de zi cu zi, care oferă un magazin de produse de cofetărie cele mai mari venituri.

Desigur, acest lucru este pur și simplu un studiu de caz. Este puțin probabil că există un magazin de patiserie, care produce doar două tipuri de produse, și cu greu cele mai mari venituri - în scopul muncii sale. Noi lucrăm un model matematic al problemei.

sunt țintă:

x - zi plăcinte foaie de parcurs;

în - prăjituri zi foaie de parcurs.

În acest exemplu poate fi numit resurse de producție? Din faptul, după cum se menționează în declarația problemă este:

durata zilei de lucru - 8 ore;

Capacitatea de depozitare - 700 locuri de cazare.

Se presupune că pentru simplitate celelalte resurse (materii prime, energie electrică și așa mai departe.) Nu sunt limitate. Formalizarea goluri - maximizând departamentul de venituri - vom discuta mai târziu.

Obținerea de relații, următoarele condiții de constrângeri de timp, magazinul de lucru și de depozitare capacitate, adică numărul total de articole.

Dintre condițiile problemei, rezultă că fabricarea de produse de patiserie uzat de 4 ori mai mult decât realizarea unei plăcintă. Dacă notăm plăcintă de fabricație - T min, timpul de producție va fi egală cu minute tort 4T. Deci, timpul total de plăcinte și prăjituri producătorului este:

TH + 4TY = (x + 4y) t.

Dar, de data aceasta nu poate fi mai lungă decât durata zilei de lucru. Rezultă din inegalitatea

Este ușor să se calculeze T - momentul fabricării de plăcintă. În ceea ce privește timpul de 1000 de bucăți pot fi făcute, atunci pateu petrecut 480/1000 = 0,48 min. Substituind această valoare în inegalitatea, obținem;

(X + 4y) · 0,48 <= 480.

Restricții privind numărul total de produse oferă o inegalitate evidentă complet:

Cele două inegalități primite trebuie să adăugați termeni de valori pozitive ale lui x și y (nu poate fi un număr negativ de plăcinte și prăjituri). Ca rezultat, vom obține un sistem de inegalități:

Și acum pentru formalizarea obiectivelor strategice: maximizarea veniturilor. Venituri - este valoarea tuturor produselor vândute. Să presupunem că prețul unei plăcintă - ruble r. Potrivit problemei, prețul de tort de două ori, adică de ruble 2r.

Vom lua în considerare expresia scrisă ca funcție de x, y:

Aceasta se numește funcția obiectiv.

Deoarece valoarea lui r - a, valoarea maximă constantă a f (x, y) este atinsă la valoarea maximă (x + 2y). Prin urmare, ca funcție obiectiv poate fi luată:

f (x, y) = x + 2y.
Prin urmare, pentru a obține un plan optim fiert până la următoarea problemă matematică: pentru a găsi obiective de valoare x și y satisfac inegalitățile sistemului“. sub care funcția obiectiv „are o valoare maximă.

Astfel, modelul matematic al planificării optime pentru patiseria școală construit.
disciplina matematică, care este dedicat pentru rezolvarea unor astfel de probleme, numit programare matematică. Deoarece funcția obiectiv f (x, y) x și y sunt liniar (adică, în primul grad), problema noastră se referă la secțiunea acestei științe numită de programare liniară.

Sistemul de inegalități scrise mai sus apare pe patrulaterul de coordonate plane. delimitată de patru linii drepte ce corespund ecuațiilor liniare:

x + y = 700;
x = 0 (axa y);

Fig. 2.19, această zonă este un ABCD patrulater și a subliniat umple. Orice punct al patrulaterului este soluția unui sistem de inegalități. De exemplu, un astfel de punct este punctul cu coordonatele x = 200, y = 100. corespunde valorii functiei obiectiv f (200100) - 400. Un punct x = 600, y = 50 corespunde

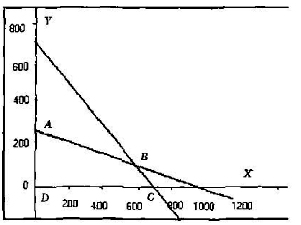
Fig. 2.19. Zona de căutare un plan optim

f (600,50) = 700. Dar, evident, soluția dorită este punctul ABCD un domeniu la care este maximizată funcția obiectiv. Găsirea acest punct este realizată folosind metode de programare liniară.

Aceste practici sunt în MS Excel arsenalul matematic în secțiunea următoare vă va învăța cum să le folosească.

Cele mai importante caracteristici

Planificarea optimă este de a identifica valorile obiective Având în vedere resursele limitate, sub rezerva realizării obiectivului strategic.

resursele limitate reprezentate matematic ca un sistem de inegalități.

Formalizarea obiectivelor strategice reduce la construcția funcției obiectiv și scopul anumitor condiții pentru amploarea ei, cel mai adesea realizarea maxim sau minim.

Programarea matematică - o ramură a matematicii, conținând metode de rezolvare a problemelor de planificare optimă.

Programarea liniară - o ramură a programării matematice, de rezolvare a problemelor de planificare optimă cu funcție obiectiv liniar.

Întrebări și Sarcini

1. a) Care este problema planificării optime?

b) Care sunt obiectivele, resursele, obiectivul strategic? Dă exemple.

b) Care este programarea matematică, programare liniară?

3.a) Formulați problema planificării optime a aceluiași magazin de patiserie școală dll, care produce trei tipuri de produse: plăcinte, prăjituri și biscuiți.

b) Faceți o schimbare în formularea planificării optime de fire 17 pentru două tipuri de produse pentru a satisface chiar și una condiții de constrângere: numărul de prăjituri nu trebuie să fie mai mic decât numărul de plăcinte. Pe plan de coordonate, vă construi soluția de căutare.

Semakin IG Henner EK Computere și TIC, 11

Trimis de cititorii site-uri web

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.