matrice algebra liniara

Inversa Matricea 13

Locul 16

Independența liniară 21

Un sistem de liniar ecua 24

Metode pentru sisteme de ecuatii liniare 27 rezolvare

27, metoda matricei inverse

Metoda pentru sisteme de ecuatii liniare cu matrice pătrată de rezolvare prin regula lui Cramer 29

Metoda (Metoda de eliminare succesivă a variabilelor) gauss' 31

matrice Razmeramhn- este un tabel dreptunghiular de numere, soderzhaschayamstrok instolbtsov. Numerele care alcătuiesc matrice, numit elementele matricei.

Matricele sunt de obicei notate cu litere majuscule latine, și elemente - la fel, dar cu litere mici, cu o indexare dublă.

De exemplu, considerăm o matrice A de dimensiune 2 x 3:

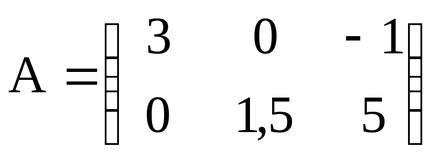
În această matrice a două rânduri (m = 2) și trei coloane (n = 3), adică Se compune din șase elementovaij. număr gdei- linie, j - numărul coloanei. În acest caz, ia valori de la 1 la 2 și de la unu la trei (înregistrate

). Și anume, a11 = 3; a12 = 0; a13 = -1; a21 = 0; a22 = 1,5; a23 = 5.

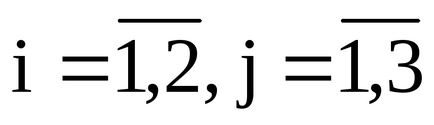
Matricele A și B sunt aceeași dimensiune (M x N) nazyvayutravnymi. dacă acestea sunt același element cu element, t.e.aij = bij pentru

, și anume pentru lyubyhiij (poate zapisati, j).

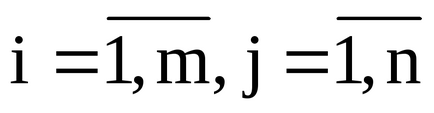
Matrix-string - o matrice formată dintr-un rând, coloană amatritsa - o matrice formată dintr-o singură coloană.

De exemplu, - un rând matrice și

.

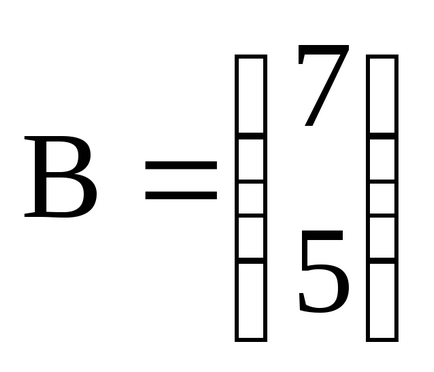
matrice pătratică de ordinul n-lea - o matrice într-un număr egal cu numărul de rânduri și coloane este egal cu n.

De exemplu,

- de ordinul doi matrice pătrată.

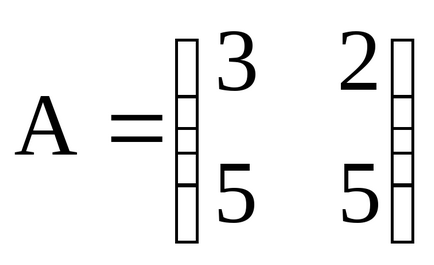
Elementele diagonale ale matricei - elementele al căror număr rând este egal cu numărul coloanei (aij, i = j). Aceste elemente obrazuyutglavnuyu matrice diagonală. In exemplul anterior, principala formă diagonală elementya11 = 3 5 = ia22.

Matricea diagonală - o matrice pătrată, în care toate elementele off-diagonale sunt egale cu zero. De exemplu,

- matrice diagonală de al treilea ordin. Dacă toate elementele diagonale sunt egale cu una, atunci nazyvaetsyaedinichnoy matrice (de obicei, notate cu litera E). De exemplu,- a treia comandă matrice unitate.

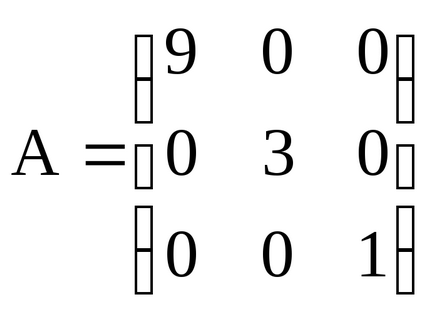
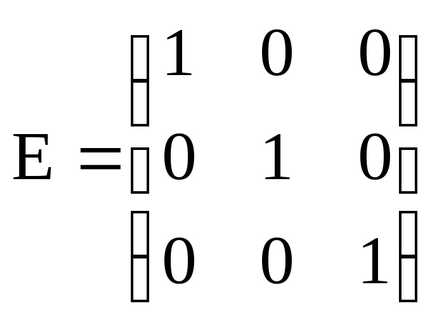
O matrice se numește zero. în cazul în care toate elementele sale sunt zero.

Matricea pătrat se numește triunghiulară. în cazul în care toate elementele de mai jos (sau peste) diagonalei principale sunt egale cu zero. De exemplu,

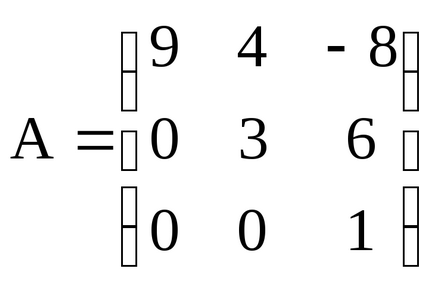
- matrice triunghiulară treilea ordin.

matrici manipulând

Pe matrici se poate efectua următoarele operații:

1. Multiplicarea unei matrice printr-un număr. Produsul a matricei A pe matricea elementelor B = chislonazyvaetsya A kotoroybij = aij pentru lyubyhiij.

De exemplu, dacă

, .

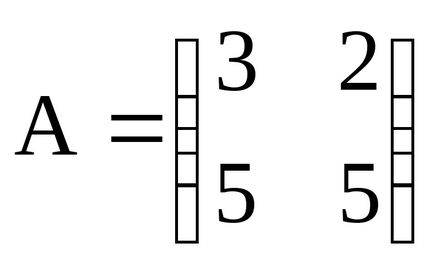
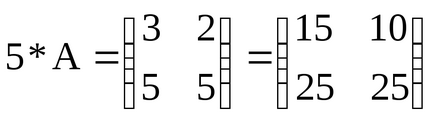
2. Adăugarea de matrici. Suma a două matrici A și B de dimensiuni egale m x n este matricea C = A + B, ale cărui elemente Sij = AIJ + dlyai bij, j.

De exemplu, dacă

.

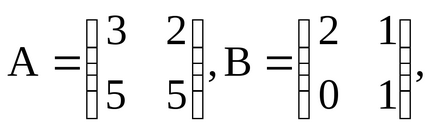
Rețineți că în operația anterioară poate fi determinată matrici scădere de aceeași mărime: diferența A-B = A + (-1) * B.

3. Multiplicarea matrici. Produsul matricei A razmeramxnna matrice razmeranxpnazyvaetsya B este o matrice C, fiecare element Sij este egal cu suma produselor elementelor i-lea rând al matricei A corespunzând elementyj-lea coloană a matricei B, adică ..

, dimensiunea produsului matrice este de 2 x 3, și va avea forma:

În acest caz, matricea A este coerentă cu W. matrice

Pe baza funcționării multiplicare pentru matricilor pătrate definite funcționare exponentiation. Un grad de întreg pozitiv m (m> 1) o matrice pătrată O m matricelor este produsul egal cu A, și anume

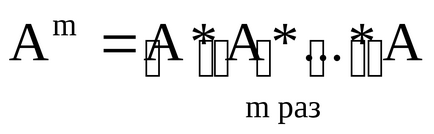
Subliniem că adăugarea (scădere) și multiplicarea matricelor nu este definit pentru două matrice, ci numai pentru a satisface cerințele specifice ale dimensiunii sale. Pentru a găsi suma sau diferența dintre dimensiunea matricei trebuie să fie aceeași. Pentru a găsi numărul de coloane ale matricei produsului de prima dintre ele ar trebui să se potrivească cu numărul de linii secunde (astfel de matrice coerentă este numită).

Luați în considerare unele dintre proprietățile de operațiuni considerate analoage proprietăților operațiilor pe numere.

1) este () legea plus comutativ comutativ:

2) asociative (asociative) legea adăugării:

(A + B) + C = A + (B + C)

3) Distribuția (distribuție) legea multiplicării peste plus:

5) asociativ (asociativă) dreptul de multiplicare:

Subliniem că legea comutativă de multiplicare a matricelor, în general, nu este îndeplinită, și anume, AB BA. Mai mult decât atât, existența OA nu implică în mod necesar existența VA (matricea poate să nu fie coerente, iar apoi produsul lor nu este determinată în general, la fel ca în exemplul de mai sus de matrice de multiplicare). Dar, chiar dacă nu există ambele produse, acestea sunt, de obicei diferite.

În cazul particular al unui produs drept comutativ are fie o matrice pătratică A de matricea identitate aceeași ordine, iar acest produs este egal cu A (multiplicarea matricea identității este similară cu unitatea de multiplicare când numerele de multiplicare):

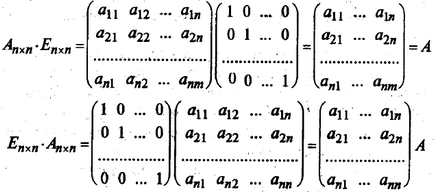
Subliniem încă o matrice de multiplicare diferență de la înmulțirea numerelor. Produs al numerelor poate fi zero, dacă și numai dacă cel puțin una dintre ele este zero. Pe matrice care poate fi spus, că produs de matrice nenulă poate fi egal cu matricea zero. De exemplu,

Vom continua luarea în considerare a operațiunilor de matrice.

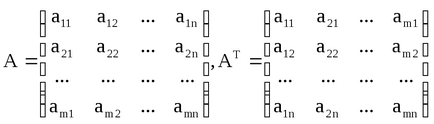
4. Matricea Transpunerea este o tranziție de funcționare a matricei A T O matrice razmeramxnk razmeranxm în care sunt schimbate rânduri și coloane:

%.

Proprietăți transpune funcționare:

1) Din definiția rezultă că dacă matricea transpune de două ori, vom reveni la matricea originala: (A T) T = A.

2) Factorul constant poate fi luată în afara transpunerii (A) ​​T = T A.

3) distributiv Transpunerea în ceea ce privește adăugarea și multiplicarea matricilor: (AB) T = B T A T și (A + B) T = B T + A T.