Liniare, pătratice, și funcția de putere soluții exemple
Graficul funcției original este o parabolă. Deoarece ecuația

convenabil de a utiliza coordonatele a două puncte de intersecție ale unei parabole cu axa abscisei și coordonatele vârful parabolei.
Noi găsim rădăcinile unei ecuații pătratice. Acestea sunt valori

Astfel, punctul de intersecție cu abscisa

Abscisa din vârful parabolei este situat la jumătatea distanței dintre punctele de intersecție cu axa parabolei

În consecință, valoarea abscisa vârful parabolei este:

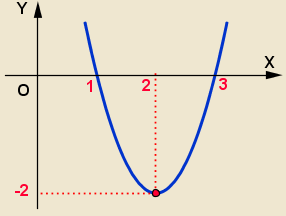
Substituind valoarea găsită în expresia funcției, vom găsi vârful ordonator al parabolei:

Astfel, vârful parabolei este punctul

Pentru rezultate trei puncte am complot parabolei.
observaţie:
Atunci când construirea de multe ori folosesc punctul grafic de intersecție cu axa y. Pentru această valoare inițială este substituită ecuația


Graficul funcției trinom poate fi construit folosind transformări elementare ale graficului

În acest caz, transformarea constă în următoarele etape.