Lecția - sinus și cosinus a sumei argumentelor
O scurtă descriere a documentului:
În cursul studierii studenților trigonometrie au fost expuse la funcțiile proprietăților lor de bază, comportamentul personajului. Printre aceste funcții principale sunt funcții periodice ale sinus, cosinus, tangentă și cotangentă. Ei au perioade și specificații diferite.
Elevii au învățat să construiască grafice și funcțiile de analiză a datelor. Domeniul studiat, valori de domeniu, creșterea și descreșterea lacunelor și m. P.
Una din formula fundamentală de bază este suma sinusul și cosinusul sumei, care sunt adesea folosite în rezolvarea diferitelor probleme. Atunci când temele, sau o varietate de elevi independenți și de control lucrări vor fi, fără îndoială, se confruntă cu necesitatea de a utiliza datele formula. Prin urmare, este important să înțelegem corect această lecție, pentru o mai bună și mai amintesc.
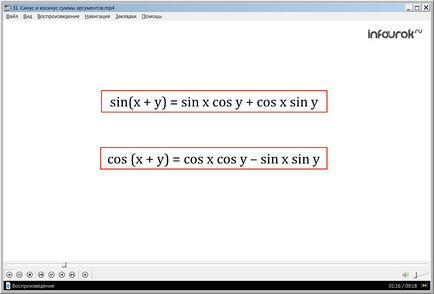
aceste formule sunt încercuite în roșu, subliniind astfel importanța amintirii va fi demonstrat în prima parte a prezentării. Vedem că acestea diferă unul de altul. Amintiți-vă de formula nu va fi dificil, dacă sunt aplicate în mod corespunzător în practică.
Crainicul a explicat elevilor modul în care doriți să citiți corect aceste formule. Unii profesori cer elevilor să joace în forma verbală a acestor formule, cu scopul de a dezvolta un limbaj matematic. Deci, ar trebui să asculte cu atenție la difuzor și înregistrează-l dacă este necesar, într-un notebook.
In urma este primul exemplu practic. Doriți să găsiți sinusul de 105 de grade. Vorbitor oferă soluții pentru acest exemplu rezultat într-un unghi de 105 de grade ca suma a două unghiuri, respectiv 45 și 60, Sines și cosinus care elevii cunosc și pot aminti că a adresat tabelul de valori ale funcțiilor trigonometrice.
Aceste tabele sunt în scopul memento-uri sunt afișate. Evidențiat valorile pe care avem nevoie. amintit în continuare formula cantitate argument sine, care este utilizat pentru rezolvarea exemplu suplimentar. În etapa finală valorile specifice sunt substituite în tabel, și se obține un răspuns.
Al doilea exemplu propune simplificarea unei expresii complex care conține funcții trigonometrice. Pentru a rezolva problema folosind ambele formule discutate mai devreme. Soluția este demonstrată pas cu pas. Că elevii să înțeleagă în cazul în care sunt valorile afișate un tabel de valori trigonometrice și scoate în evidență celulele utilizate.
Ca rezultat, la fel ca în exemplul anterior, este afișat răspunsul.
Al treilea exemplu este similar cu primul, al patrulea și având în vedere în continuare decizia este mai complicată și interesantă. Trebuie să găsești cosinusul suma argumentului, dacă știți că unele dintre date. De preferință ia în considerare problema cu profesorul sau tutorele. În cazul în care un student este inteligent și un cadru matematic bun, el va fi capabil să înțeleagă și în mod independent, în cazul în care lecția pierdut sau doriți să-l restaureze în memorie. În scopul de a consolida înțelegerea acestor exemple, putem oferi studenților câteva alte exemple similare din manualul școlar, soluția pe care vor trebui să utilizeze formula de suma sinus și cosinus a argumentelor.
Un al cincilea exemplu de complexitate ocupă primul loc. Se propune să rezolve ecuații trigonometrice, care trebuie să fie bun să-și amintească și să înțeleagă modul în care utilizați formule trigonometrice.
Decizia este foarte clar și mod detaliat. Crainicul explică fiecare pas, nu pierde nici un moment important. Pe partea dreaptă a soluțiilor conținute bule și formule care se aplică atunci când efectuează lucrarea.
Suntem deja familiarizați cu funcțiile trigonometrice, graficele lor, au învățat să rezolve ecuații trigonometrice. Și acum trece la studiul de formule trigonometrice prin care ne transforma expresii trigonometrice.
Cele mai importante sunt formula trigonometrie, denumit în mod obișnuit ca suma sinus și cosinus sumei.
sin (x + y) = sin x cos y + cos x păcat y,
cos (x + y) = cos x cos y - sin x păcat y.
Aceste ecuații pot fi citite ca suma a două unghiuri sinusoidale este egal cu suma produsului dintre sinusul și cosinusul unghiului de primul unghi și al doilea produs al cosinusul și sinusul primul colț al doilea unghi;
cosinusul suma a două unghiuri este egală cu diferența dintre produsul din cosinusul acestor unghiuri și produsul dintre suma acestor unghiuri.
Din aceste formule putem obține aproape toate formulele de trigonometrie.
Cum se utilizează aceeași formulă suma sinus și cosinus a sumei. Luați în considerare exemplele date pe care fiecare formulă poate fi aplicată ca „stânga“ și „dreapta“.
Exemplul 1. Calculati păcat 105 °.
Decizie. Reprezintă o sută cinci grade ca suma de 105 ° = 45 ° + 60 °. Noi știm că păcatul de 45 ° = cos 45 ° =. păcat 60 ° =. cos 60 ° =.
Afișare tabel de valori
Substituind aceste valori în formula pentru suma sine
sin (x + y) = sin x cos y + cos x păcat y,
Togdasin 105 ° = sin (45 ° + 60 °) = sin 45 ° cos 60 ° + 45 ° cos păcat 60 ° = ∙ + ∙ = =.
(O sută cinci grade sine este sinusul sumei de patruzeci și cinci de grade și șaizeci de grade și este egală cu această fracție sumă, numărătorul care este rădăcina suma celor două, și rădăcina de șase, iar numitorul -. Patru)
Răspuns: păcat 105 ° =.
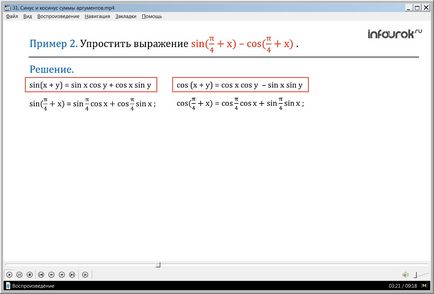
Exemplul 2. Pentru a simplifica păcatul expresie (+ x) - cos (+ x) (diferența pi sine împărțit la patru, plus X și cosinusul pi împărțit la patru, plus X).
Decizie. Se aplică formula sine pentru păcat cantitate redusă (+ x)
sin (x + y) = sin x cos y + cos x păcat y,
Apoi reduce sin (+ x) = sin + cos sinh cosh.
Se aplică formula la suma cos cosinus Scăzător (+ x)
cos (x + y) = cos x cos y - sin x păcat y.
cos Scăzător (+ x) = cos + sin cosh sinh
sin (+ x) - cos (+ x) = sin cos x + cos sin x - cos cos + sin sin x x
Afișare tabel de valori
Din valorile din tabelul găsi valoarea păcatului și cos
sin =, cos =, substituie aceste valori în expresia și se obține:
= ∙ + ∙ cosh sinh - ∙ + ∙ cosh sinh
Cosh ∙ - ∙ = 0 cosh, Sinh este ∙ + ∙ Sinh, care este de 2 ∙ ∙ Sinh Sinh get.
sin (+ x) - cos (+ x) = sin cos x + cos sin x - cos cos + sin sin x = x
= ∙ cos x + ∙ sin x - x + ∙ cos ∙ sin x = 2 ∙ ∙ sin x = sin x. Aceasta este o soluție numerică completă.
Răspunsul este: sin (x +) - cos (+ x) = sinh.
Exemplul 3. Se calculează păcatul 17 ° cos 13 ° + cos17 ° sin 13 °. (Șaptesprezece grade, Sine înmulțită cu cosinusul treisprezece grade plus cosinusul șaptesprezece grade, înmulțit cu sinusul treisprezece grade).
Decizie. Această expresie poate fi „ori“ în suma argumentelor sinus 17 ° și 13 ° (de ex. Utilizați „dreptul la stânga“ formulă sine pentru suma).
sin (x + y) = sin x cos y + cos x păcat y,
păcat cos 13 ° + sin cos 13 ° = sin (+ 13 °) = sin 30 ° = (suma produsului sinusului de șaptesprezece grade cosinusul treisprezece grade și funcționează cosinus șaptesprezece grade sinus treisprezece grade egale cu sinusul sumei de șaptesprezece și treisprezece grade egal cu sinusul treizeci grade egale cu o secundă).
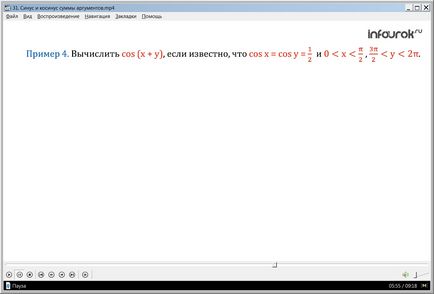
Exemplul 4. Se calculează cos (x + y), dacă știm că cos x = y = cos
0 x (X este mai mare decât zero și mai puțin de două pi) la 2p (y pi mai mult de trei de doi, dar mai puțin de două pi).
Decizie. Noi folosim formula sumei cosinus:
cos (x + y) = cos x cos y - sin x păcat y.
Valorile COSX și un set confortabil. Se calculează valorile și sinx siny. Noi folosim identitate trigonometric de bază: păcatul 2 t + cos 2 t = 1. Avem: păcat 2 x = 1 - cos 2 x. și ca x = cos. atunci înlocuim în formulă și se obține = 1 - () 2 = 1 - =.
păcatul 2 x = 1 - cos 2 x = 1 - = Această soluție completă numerică.
Prin starea argumentului X face parte din primul trimestru, și în ea sinusul este pozitiv. = De aceea Sinh.
In mod similar, păcatul 2 y = 1 - cos 2 y = 1 - =. dar argumentul y aparține al patrulea trimestru, și sine este negativ, astfel încât păcatul y = -.
Substituind valorile obținute și prezentate în formula pentru suma cosinusul obține cos (x + y) = ∙ - ∙ = + = 1.
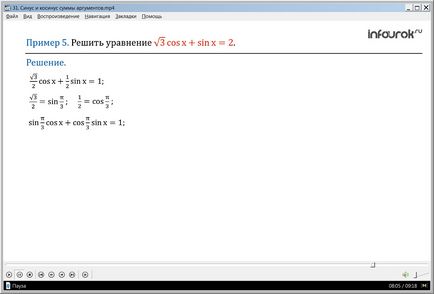
Exemplul 5 Rezolva ecuația cosx + sinx = 2.
Se împarte ambele părți de două, obținem cosx + sinx = 1
Aici este ecuația pentru forma formulă suma sinus a două unghiuri:
și reamintească faptul că = sin. a = cos.
Afișare tabel de valori
cos x + sin x = 1,
sincos x + cos sin x = 1,
Apoi, pe partea stângă a ecuației este partea dreaptă a formulei pentru suma sinus și x argumente. Astfel, partea stângă a expresiei este egală cu sin (+ x)
Noi căutam valoarea lui x