Însumare anumitor secvențe

prin urmare
1 2 + 2 2 + 3 + 2. + N = 2 (n + 3 n + 2 (1 + 2 + 3 +. + N)) / 3.

deoarece
1 + 2 + 3 +. + N = n (n + 1) / 2,
1 2 +2 2 + 3 + 2. + N = 2 (n + 3 n + 2 n (n + 1) / 2) / 3 = n (n + 1) (2 n + 1) / 6.

Suma a patra puteri ale primelor numere n primit matematicianul arabică al- Karadzhi (X-XI cc.). A construit pătrat cu laturile (1 + 2 + 3 + + (n - 1). + N). și în ea - cealaltă pătrat (adiacent la colțul primului pătrat), cu o latură (1 + 2 + 3 + + (n - 1).). Diferența dintre aceste două pătrate este gnomon a cărui n lățime. o parte mare este egal cu (1 + 2 + 3 + + (n - 1). + n) = n (n + 1) / 2. Zona gnomon 2 n 2 (n + 1) / 2 - n 3 2 = n . Dacă acum într-un pătrat cu latura de (1 + 2 + 3 + + (n - 1).) pentru a atribui aceeași lățime gnomon (n - 1). aria sa este (n - 1) 3. Continuând în acest fel, în cele din urmă ajunge la pătrat original 1. Suprafața unui pătrat cu latura de (1 + 2 + 3 + + (n - 1). + n). astfel, împărțit în gnomons, dintre care zone sunt egale cu n 3. (n - 1) 3. 3 3. 2 3. și suprafața pătrată a 1 = 1, 3. Astfel, 1 3 + 2 3 + 3 + 3. + N = 3 (1 + 2 + 3 +. + N) = 2 (n (n + 1) / 2) 2.

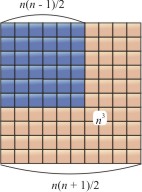
Fig. 8. Zona rănii gnomon n 3

O secvență de interesantă a considerat francez scolastic secolului al XIV-lea filozof. - N. Orem. Se întreba ce s-ar fi egală cu viteza medie (în terminologia medie „intensitate“, un termen mai general, dar acum suntem suficient pentru a considera viteza medie) intervalul este de 2, în cazul în care această perioadă este împărțită în secțiuni corespunzătoare o progresie geometrică descrescătoare: 1, 1/2, (1/2) 2 (1/2) 3. și în fiecare secțiune a crește rata într-o progresie aritmetică 1, 2, 3, 4. în scopul de a rezolva această problemă, este necesar să se evalueze expresia tip: 1 # X2219; 1 + 2 # X2219; (1/2) + 3 # X2219; (1/2) 2 + 4 # X2219; (1/2) 2. Suma numărului de Orem reprezentat ca aria figurii în trepte, din care se confruntă reciproc dreptunghiuri, fiecare dintre care are o înălțime de 1, iar lățimea fundului 2, suprapusă una suplimentară 1/2. (1/2) 2 și t. D. Întreaga figură este împărțită prin linii verticale în bucăți de o lățime de 1, 1/2, (1/2) 2 și t. D.

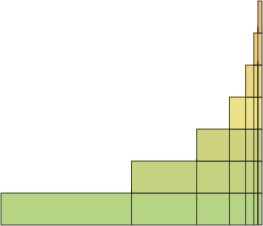
Fig. 9. Mai multe Orem

Această cifră, de fapt, nimeni altul decât graficul de viteză de înălțime, în partea sa cea mai din stânga este egal cu 1, apoi 2, apoi 3, etc. Suma unui număr egal cu aria întregii figura, împreună cu faptul că zona poate fi găsit într-un mod diferit ..: aria dreptunghiului este egal cu 2, o mai mare de 1, apoi 1/2 (1/2) 2, etc. - .. nu avem de a face cu altceva decât o progresie geometrică, valoarea care este egală cu 4. viteza medie pe întregul interval egală cu suprafața totală (4), împărțit la lungimea diferenței (2) - adică 2, viteza a doua decalaj. Infinitul scădere progresie geometrică și numărul considerat de Orem, au o cantitate finită. Și cealaltă serie? Este clar că, pentru ca suma unui număr infinit de termeni ai seriei ar fi egală cu o valoare finită, trebuie să faci un număr de membri ar tinde la zero, adică, începând cu un număr suficient de mare pentru a deveni mai puțin decât orice valoare prestabilită specificată. Dar acest lucru nu este suficient. Există, de ei înșiși, o secvență care tinde la zero, astfel încât suma seriei tinde la infinit. Orem în primul rând pentru a dovedi că seria armonică

nu summable, adică suma membrilor săi n ca n crește, mai devreme sau mai târziu va depăși orice valoare preasigurată. Dovada se bazează pe faptul că

1/3 + 1/4> 2/4 = 1/2,
+ + 1/6 1/5 1/7 + 1/8> 1/2,

8 și următoarele numere în valoare de mai mult de 8/16 = 1/2, și așa mai departe. D. A, deoarece un număr de 1/2 + 1 + 1/2 + 1/2 + și t. D. Crește în mod evident la infinit, și seria armonică, de asemenea, merge la infinit. Acest fapt este uneori ilustrată după cum urmează.

Cărămizile sunt plasate unul peste altul, astfel încât acestea nu se încadrează: pentru acest centru de masă a cărămizilor superioare trebuie să se afle în interiorul bazei inferioare. În cazul în care două cărămizi, poate fi deplasat în raport cu cealaltă jumătate lungime. În cazul în care trei, apoi mijlocie în raport cu partea de jos pentru a fi mutat cu un sfert, pentru că centrul de masă dintre cele două este situat la jumătatea distanței dintre centrele de masă din fiecare. În cazul în patru, apoi în ceea ce privește partea de jos a cărămida următoare să fie deplasat de-a șasea lungime de o cărămidă. Și așa mai departe. D. În general, se pare că, cu un număr nelimitat de cărămizi ideale, în partea de sus poate fi deplasat în raport cu partea de jos pe orice distanta, ca serie armonică poate avea o valoare mare în mod arbitrar.

În plus față de sumele fără sfârșit pot fi considerate produse infinite. Prima dintre ele a introdus de F. Wyeth. Având în vedere problema cvadratura cercului, Wyeth a adus relația dintre aria unui poligon regulat cu n și 2 n laturi înscris în același cerc de rază R. Fiecare dintre aceste poligoane pot fi împărțite în 2 n triunghiuri cu vârful în centrul unghiului poligon și vertex, egală cu 180 ° / n. la primul dintre ele, fiecare astfel de triunghi este dreptunghiular, iar al doilea isoscel. Pentru că ei au o înălțime comună, raportul dintre zonele lor este egală cu raportul dintre baze. Cos R întâi de bază (180 ° / n). al doilea raport al suprafeței R. poligoane egală cu raportul ariilor acestor triunghiuri t. e. cos (180 ° / n).

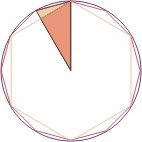
Fig. 10. Raportul suprafață este raportul dintre bazele triunghiuri