Funcția pătratică 3

trinomial Square este un grad polinom al doilea, care este o expresie a forma ax 2 + bx + c. în cazul în care un ≠ 0, b. c - (de obicei, predeterminate) numere reale, numite coeficienți săi, x - variabila.

Notă: un raport poate fi orice număr real altul decât zero. Într-adevăr, în cazul în care a = 0, atunci ax 2 + bx + c = 0 · x 2 + bx + c = 0 + bx + c = bx + c. În acest caz, expresia nu este încă pătrat, deci nu poate fi considerat un trinom pătrat. Cu toate acestea, expresia astfel-binomi, cum ar fi, 3x 2 - 2x sau x 2 + 5 poate fi privit ca un trinom pătrat, dacă suplimentarea le lipsește monoamele cu coeficienți zero: 3x 2 - 2x = 3x 2 - 2x + 0, și x 2 + 5 = x 2 + 0x + 5.

În cazul în care sarcina este de a determina valoarea variabilei x. în care trinom pătrat devine zero, adică ax 2 + bx + c = 0, atunci avem o ecuație pătratică.

Dacă există rădăcini reale x1 și x2 unei ecuații pătratice, trinomul corespunzătoare pot fi descompuse în factori liniari. ax 2 + bx + c = a (x - x1) (x - x2)

Notă: În cazul în care trinomul pătrat considerat pe mulțimea numerelor complexe, pe care, probabil, nu ați studiat, factorii liniare pot fi extinse în orice moment.

Atunci când este o altă sarcină de a determina toate valorile care pot accepta rezultatul calculului trinomul pătrat pentru diferite valori ale lui x. și anume y definesc expresia y = ax 2 + bx + c. atunci avem de a face cu o funcție pătratică.

În acest caz, rădăcinile unei ecuații pătratice sunt zerourile unei funcții pătratice.

trinom pătrat poate fi scrisă

Acest punct de vedere este utilă atunci când reprezentarea grafică și studierea proprietăților funcțiilor pătratice ale unei variabile reale.

Funcția este o funcție pătratică dată de formula y = f (x), unde f (x) - trinom pătrat. Ie formulă de forma

în cazul în care un ≠ 0, b. c - orice numere reale. Sau converti o formulă, cum ar fi

.

Graficul funcției pătratică este o parabolă, al cărui vârf este la punctul.

Notă: Nu se spune că graficul unei funcții pătratice se numește parabole. Se spune că graficul funcției este o parabolă. Acest lucru se datorează faptului că o astfel de curbă de matematică a descoperit și numit parabolei, înainte (din pi greacă # 945; # 961; # 945; # 946; # 959; # 955; # 942; -. Comparația, comparația, similitudinea) la stadiul de studiu detaliat proprietăți și graficul funcției pătratice.

Parabolă - linia de intersecție a unui con circular drept cu un plan care nu trece prin vârful conului și paralel cu una dintre generatoarele acestui con.

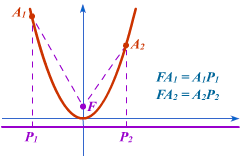
Parabolă are o altă proprietate interesantă, care este, de asemenea, utilizat ca definiția sa.

O parabolă este setul de puncte un plan a cărui distanță față de planul de la un anumit punct, numit un accent al parabolei, distanța este egală cu o anumită linie dreaptă, numită directricea unei parabole.

Construi un grafic funcție pătratică, puteți schița Keypoint.
De exemplu, functia y = x 2 puncte ia

Dar, în orice caz, punctele pot fi construite doar o schiță a graficului funcției pătratice, adică, un calendar aproximative. Pentru a construi parabolei cu precizie, trebuie să utilizați proprietățile sale: focalizarea și directricea.
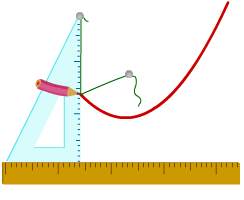
Înarmat cu hârtie, o riglă, set pătrat, două butoane și un fir puternic. Atașați un buton aproximativ în centrul unei coli de hârtie - un punct care va fi punctul central al parabolei. În al doilea rând buton, atașați la partea de sus a colțul de jos al poligonului. Pe baza de butoane fixa fir, astfel încât lungimea sa este egală între butoanele cateta mari gon. Desenați o linie dreaptă care nu trece prin punctul central al parabolei viitorului - directricea parabolei. Atașați linie la directoarei și pătrat la linia așa cum se arată în figură. Muta pătrat de-a lungul rigla în timp ce apăsați pen-ul la hârtie și la gon. Asigurați-vă că firul a fost întins.

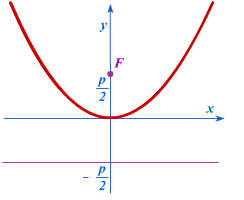
Măsurați distanța dintre punctul central și directricea (amintiți-vă - distanța dintre punctul și linia definită de perpendiculara). Acesta este parametrul focal al parabolei p. In sistemul de coordonate prezentat în figura din dreapta, ecuația noastră parabole are forma: y = x 2 / 2p. În desenul meu scara avansat grafic al funcției y = 0,15x 2.

Notă: Pentru a construi un anumit parabole într-o scară de dat, trebuie să faci aceleași lucruri, dar într-o ordine diferită. Tu ar trebui să înceapă cu axele de coordonate. Apoi, trage o directoarei și de a determina poziția central al parabolei. Și numai atunci instrument de proiectare din poligon și linia. De exemplu, pentru a construi pe hârtie în carouri unei parabole ecuație y = x 2. focalizarea trebuie plasat la o distanță de 0,5 celule din directricea.

Proprietățile funcției y = x 2

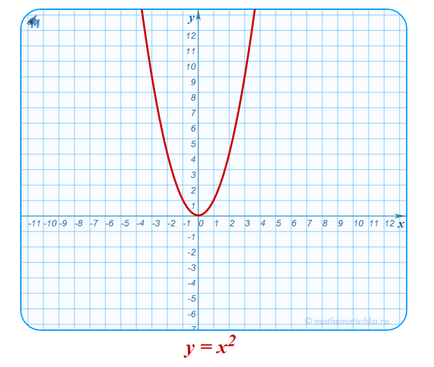
1. Domeniul funcției - linia număr întreg: D (f) = R = (-∞; ∞).
2. Valori de câmp ale funcției - cel pozitiv jumătățile: E (f) = [0; ∞).
3. Funcția y = x 2 este chiar: f (-x) = (-x) 2 = x 2 = f (x).
   Axa y este axa de simetrie a parabolei.
4. Intervalul (-∞, 0) funcția descrește monoton.
   In intervalul (0; + ∞) funcția crește uniform.
   
5. La punctul x = 0 atinge o valoare minimă.
   Punctul cu coordonatele (0, 0) este vârful parabolei.
6. Functia este continua pe domeniul său.
7. Asimptotă nu are.
8. Zerourile: y = 0 pentru x = 0.

Proprietățile unei funcții pătratice a formei generale.

1. Domeniul funcției - linia număr întreg: D (f) = R = (-∞; ∞).
2. Intervalul funcției depinde de un semn al coeficientului.
   Când a> 0 parabole ramură direcționată în sus, funcția are un minim (Ymin), dar nu are cea mai mare valoare: E (f) = [Ymin; ∞);
   cu un + bx 2 + c nu este nici măcar, nici ciudat.
   Axa de simetrie a parabolei este o linie x = -b / 2a.
   Funcția va fi chiar și numai în cazul în care această linie coincide cu axa Oy. și anume când b = 0.
3. Când a> 0 descreștere funcție monoton peste intervalul (-∞; -b / 2a) și monotonă crește pe intervalul (-b / 2a; ∞).
   La un 0 - minim de funcții.

Ambele valori sunt definite prin formula y = - b 2 - 4ac _______. 4a

Ideea este coordonatele nodurilor ale parabolei.

Functia este continua pe domeniul său.

Asimptotă nu are.

Parabolei intersectează ordonata la punctul (0; c).
Dacă trinom pătrat are deytsivtelnye rădăcini x1 ≠ x2. parabolei intersectează axa x la punctele (x1, 0) și (x2; 0).
Când x1 = x2 în abstsics axa parabolei la punctul (x1; 0).

Derivata funcției pătratică se calculează conform formulei (ax 2 + bx + c) „= 2ax + b.

Graficul funcției pătratică dată de formula generală, cel mai bun construct și studiu folosind conversie reguli grafice.
În acest scop, trebuie să treacă mai întâi de formula y = ax 2 + bx + c la o formă adecvată pentru transformare, y = m (kx + l) 2 + n. în care k, l, m, n - numărul care depind de a, b, c. și anume în minte
.
Apoi vom lua parabolei y = x 2 și aplică următoarea transformare la ea:

• transfer paralel (deplasare) în parabole l originală = b / 2a unități la stânga (când l 2 - 4ac) / unități 4a în funcție sus sau în jos pe semnul n (dacă n> 0 în sus).

Formulele pentru o astfel de tranziție pot fi învățate pe de rost, dar puteți învăța cum să aloce pătrat completă a unui trinom dat coeficienți. Această capacitate este foarte util, de asemenea, pentru rezolvarea unor ecuații și inegalități, pentru a calcula integralele etc.

Luați în considerare acest exemplu:
Să y = 3x 2 - 5x + 2
1) Se combină între paranteze primele două termeni și scoate coeficientul de paranteze x 2.
2) In paranteze se multiplica si divide cu 2 simultan coeficientul lui x.
3) compară construcția binomial formula într-un pătrat: parantezele pătrate au în număr x. de două ori produsul x prin fracția 5/6. Pentru a aplica această formulă este lipsită de al doilea pătrat, deci adăugați termenul lipsă este de 5 2/6 2 și scade-l în același timp, pentru a păstra valoarea originală a expresiei.
4) Stingem pătrat de formula și dezvăluie paranteze mari.
5) Fracțiunile numerice rămase prezintă un numitor comun și se adaugă în sus.

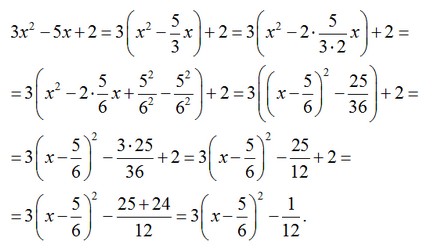
Deci, pentru a construi un grafic al funcției y = 3x 2 - 5x + 2 din graficul y = x 2 este de a fi ultima mutare a Ox-axa spre dreapta 5/6 ≈ 0,83 unități. Apoi se întind de-a lungul axei Oy de 3 ori și în final coborâtă cu axa Oy, la 1/12 ≈ 0,08 unități.
Uite ce sa întâmplat.

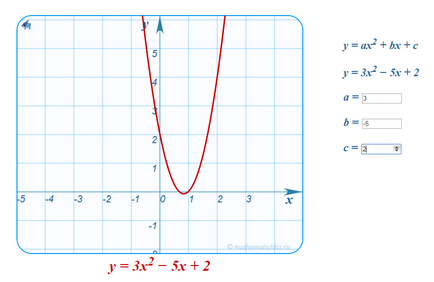
Dacă sunteți un student de-al meu, sau abonat. puteți lucra cu versiuni interactive ale acestor grafice.

Exercițiu:
Constructul punctele caracteristice ale graficului schiță y = x 2.
Metoda de conversie va primi un grafic schiță a unei funcții y = -x 2 + 4x + 6.
Uita-te la ce punctează graficul acestei funcții se intersectează cu axa Ox și să compare coordonatele (Abscisa) din rădăcinile ecuației 2 -x + 4x + 6 = 0. calculat de discriminante. Cât de precisă este soluția grafică dovedit din ecuație?

Noi transformăm expresia cu lansarea unui pătrat perfect:

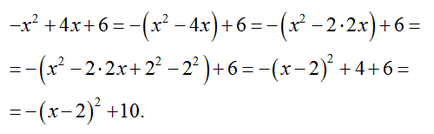
Construirea unui grafic al funcției
.

Pentru aceasta utilizați următorii pași: deplasarea la dreapta 2-celule, rândul său, ramuri (vârf - un punct în raport cu care pivotat), pentru a ridica partea de sus și, respectiv, întreaga parabole de până la 10 celule. Iată ce ar trebui să aveți

.

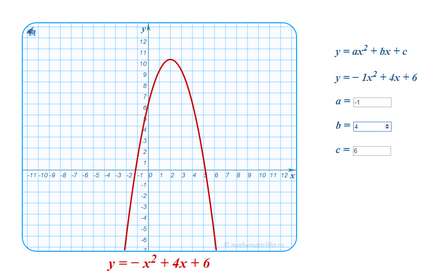
definesc vizual rădăcini. Parabolă intersectează axa Ox cu aproximativ o cincime din celule la stânga minus unu și aceleași drepturi ca și cele cinci, și anume x1 ≈ -1,2. x2 ≈ 5,2.

Soluția conform formulelor de constatare a rădăcinilor unei ecuații pătratice dă răspunsuri x1 = 2 - √10 __. x2 = 2 + √10 __.
Calculatorul compute x1 = -1,162277660. x2 = 5,162277660.

Parabolă - curba foarte interesantă, o funcție pătratică este adesea găsit în descrierea diferitelor fenomene naturale, procesele economice.

Grafice de funcții pătratice și coeficienții trinomul pătratică.

Poziția și forma parabolei în funcție de semnul și valoarea coeficientului și - coeficientul lui x 2.

Poziția și forma parabolei în funcție de semnul și valoarea coeficientului b - coeficientul pentru x.

Poziția și forma parabolei în funcție de semnul și valoarea parametrului c.

Provocări pentru analiza graficului unei funcții pătratică.

Sarcini precum „Set de corespondență între coeficienții de trinom pătratic și graficele funcțiilor pătratice“ se găsesc în JEG matematică în clasa a noua, precum și nevoia de predare a examenului pentru gradul 11 ​​ca o acțiune intermediară.