Ecuația cu trei necunoscute, matematica

62. O ecuație cu trei necunoscute. Să presupunem că avem o ecuație

În această ecuație poate fi privit ca un record de sarcini: pentru a găsi valori numerice pentru x, y și z, la trinomial 3x + 4y - 2z a fost egal cu numărul 11. Deci, aceasta este o ecuație cu trei necunoscute. Deci, cum putem rezolva o ecuație cu o singură necunoscută, care la prima vedere există ideea că există două necunoscute, cum ar fi de prisos, și ele pot fi date valori arbitrare. Într-adevăr, în cazul în care, de exemplu, să ia un număr y 3 și z numărul 5, obținem ecuația într-o singură necunoscută:

Ia alte numere pentru y și z. De exemplu, să

Atunci vom obține ecuația:

Continuând această lucrare pe, am ajuns la concluzia:

O ecuație cu trei necunoscute, are infinit mai multe soluții, și pentru ei este necesar să se dea două valori arbitrare necunoscute.

Rezultatele acestei lucrări pot fi scrise în tabel (exceptam celor două soluții deja găsite, înregistrate în ea este o alta, care se obține prin punerea y = -1 și z = -2):

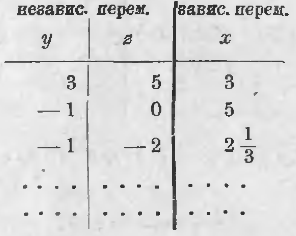
Deoarece y și z pentru luăm valori arbitrare, ele sunt variabile independente, iar x este dependentă (de) o variabilă. Cu alte cuvinte: x este o funcție de y și z.

Pentru a face mai ușor pentru a obține soluția acestei ecuații, ea poate fi determinată de la x de y și z. obținem:

3x + 4y - 2z = 11; 3x = 11 - 4y + 2z;
x = (11 - 4y + 2z) / 3.

Noi da, de exemplu. valori: y = 5 și z = 1; obținem: x = (11 - 20 + 2) / 3 = -2 (1/3), etc ...

Să luăm ecuația

Să presupunem că x și y ca variabile independente și z - dependențe și defini z prin x și y

2Z = 7 - 3x + 5y; 2z = 3x - 5y - 7; z = (3x - 5y - 7) / 2

Acum, este ușor de a face un tabel de decizie: