Cum de a rezolva un sistem de ecuații cu două necunoscute

Metoda de adăugare.
două ecuații trebuie să fie scrise strict sub reciproc:

Apoi, ori fiecare termen de ecuații, respectiv, luând în considerare semnele lor:

2 + (- 9X) = - 7x, -5u 5y + 0 = 61 + (- 40) = 21. De obicei, una dintre sumele care conține o valoare necunoscută va fi zero.






Scrieți ecuația membrilor rezultate:

-7x + 0 = 21.
Găsiți necunoscute: 7h = 21, h = 21 (- 7) = - 3.
Substitut găsit deja valoarea în oricare dintre ecuațiile și începe să primească al doilea necunoscut, rezolvarea ecuației liniare:

2-5u = 61, 2 (-3) = -5u 61 -6-5u = 61 + 61 = -5u 6 -5u = 67, y = -13.4.
Răspunsul este sistemul de ecuații: x = -3, y = -13.4.

metoda de substituție.
Dintr-o ecuație trebuie să exprime oricare dintre membrii necesare:

x + 5y = 61, x = 61 + 5y.
Pentru a înlocui ecuația obținută în al doilea în locul numărului „X“ (în acest caz):

ecuație liniară pentru a găsi numărul „y“:

-549 + 45u + 4y = -7, 45u + 4y = 549-7, 49U = 542, y = 542: 49, u≈11.
In alese aleatoriu (out) în locul ecuației inserați deja găsit numărul „y“ al doilea 11 și se calculează necunoscut:

X = 61 * 11 + 5, x = 61 + 55 = 116 x.
Răspunsul dat sistem de ecuații: x = 116, y = 11.

mod grafic.
Este găsirea coordonatelor practice punctuale care se suprapun direct înregistrate matematic în ecuațiile sistemului. Este necesar să se traseze graficele atât directă, separat, în același sistem de coordonate. Vedere generală a ecuației este simplă: - y = kx + b. Pentru a construi linia, este suficient pentru a găsi coordonatele a două puncte, și, x este ales la întâmplare.
Având în vedere un sistem: 2x - y = 4

-3H- + y = 1.
Construit chiar pe prima ecuație, pentru comoditate trebuie să fie scris: y = 2x-4. Vino valori (mai ușoare) pentru X, înlocuind-o în ecuație, rezolvare, pentru a găsi y. S-a obținut două puncte, care orientează construcții. (Vezi fig.)
0 x 1

y -4 -2
Construit chiar pe a doua ecuație: y = -3H- + 1.
Doar construi linia. (Vezi fig.)

y 1 -5
Găsiți coordonatele punctului de intersecție a două linii drepte construite pe diagramă (în cazul în care liniile nu se intersectează, atunci sistemul nu are nici o soluție - se întâmplă).

Pentru a rezolva un sistem de ecuații cu două variabile sunt utilizate în mod obișnuit următoarele metode: metoda grafică, substituția și metoda de adăugare. Locui la prima dintre realizările de mai sus.

Luați în considerare secvența de soluții ale sistemului, care este format din ecuații liniare ale formei: a1x + b1y = c1 și a2x + b2y = c2. Acolo unde x și y - variabile necunoscute, și b, c - termenii liberi. La aplicarea acestei metode fiecare sistem de soluție este o directă de puncte de coordonate corespunzătoare fiecărei ecuații. Pentru a începe cu, în fiecare caz, exprimă o variabilă peste alta. Apoi setați variabila x orice mai multe valori. Este suficient să două. Membru supleant în ecuație și pentru a găsi y. Construiți un cadru de referință, marca punctele obținute pe ea și rula direct prin intermediul lor. Calcule similare trebuie efectuate pentru alte părți ale sistemului.

Punctul sau punctele de intersecție ale graficelor construite și va fi o soluție a acestui set de ecuații.

Sistemul are o soluție unică în cazul în care liniile construite se intersectează și au un punct comun. Este inconsecvent, dacă grafica sunt paralele între ele. Și are o infinitate de soluții, atunci când îmbinarea directă unele cu altele.

Această metodă este considerată a fi foarte clar. Principalul dezavantaj este faptul că necunoscutele calculate sunt valori aproximative. Un rezultat mai precis este dat așa-numitele metode algebrice.

Orice soluție a sistemului este în valoare de verificat. Pentru a face acest lucru, înlocuiți variabilele valorile obținute. Puteți găsi, de asemenea, soluția în mai multe moduri. În cazul în care soluția sistemului de drept, toate răspunsurile ar trebui să obțineți același.

De multe ori există ecuații în care unul dintre termenii nu este cunoscut. Pentru a rezolva această ecuație, trebuie să ne amintim și să fie făcut cu numere date un anumit set de acțiuni.

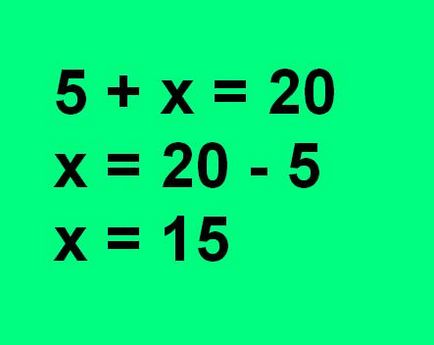
Soluția sistemelor - o secțiune destul de complicată din programa școlară. Cu toate acestea, în realitate, există unele algoritmi simpli care vă permit să faceți acest lucru rapid. Unul dintre ei - o soluție adăugarea de sisteme de metodă.

Sistemul de ecuații liniare este o combinație a două sau mai multe ecuații, fiecare dintre care are două sau mai multe necunoscute. Există două modalități principale de sisteme de ecuații liniare, care sunt utilizate în programa școlară de rezolvare. Una dintre ele se numește metoda de substituție, celălalt - metoda de adăugare.

Forma standard a sistemului de două ecuații

In forma standard a primei ecuații este de forma a1 * x + b1 * y = c1, a doua ecuație este a2 * x + b2 * y = c2, și așa mai departe. De exemplu, în cazul unui sistem cu două părți, în ambele ecuațiile de mai sus a1, a2, b1, b2, c1, c2 - sunt coeficienți numerici, prezentate în ecuațiile specifice. La rândul său, x și y sunt necunoscute, valorile care trebuie determinate. Plătiți valorile necesare ale ambelor ecuații simultan în adevărata egalitate.

Decizia înseamnă sistemul plus

Pentru a rezolva adăugarea înseamnă un sistem care este de a găsi valorile lui x și y, care le va transforma într-o adevărată egalitate, este necesar să se ia câțiva pași simpli. Prima dintre ele este de a converti toate ecuațiile, astfel încât coeficienții numerice pentru variabila x sau y în ambele ecuații este aceeași în mărime, dar diferă în semn.

De exemplu, să presupunem că avem un sistem format din două ecuații. Prima dintre acestea are forma 2x + 4y = 8, a doua formă are 6x + 2y = 6. Una dintre sarcina celui de al doilea exemplu de realizare este coeficientul de multiplicare pentru ecuația 2, care îl va conduce la -12x-4y = -12 minte. Alegerea corectă a coeficientului este una dintre sarcinile cheie în procesul de adăugare a procesului de soluție, deoarece determină întregul curs viitor de a găsi procedura de necunoscut.

Acum este necesar să se efectueze adăugarea a două sisteme de ecuații. Evident, distrugerea reciprocă a variabilelor egale în valoare, dar opuse în semn de coeficienții va conduce la forma -10x = -4. După care aveți nevoie pentru a rezolva o ecuație simplă, din care arată în mod clar că x = 0,4.

Pasul final în procesul de soluție este substituirea valoarea găsită pentru una dintre variabilele în oricare dintre ecuațiile originale disponibile în sistem. De exemplu, prin substituirea x = 0,4 în prima ecuație, putem obține expresia 2 * 0,4 + 4y = 8, unde y = 1,8. Astfel, x = 0,4 și y = 1,8 rădăcinile sunt furnizate în sistemul de exemplu.

Pentru a se asigura că rădăcinile au fost găsite adevărate, este util să se facă de verificare prin înlocuirea valorilor găsite în a doua ecuație a sistemului. De exemplu, în acest caz, egalitatea se obține sub formă * 6 + 0,4 1,8 * 2 = 6, ceea ce este adevărat.