Cum de a reduce fracțiile la gradul

Pentru a fara probleme pentru a reduce fracțiunea la un anumit grad, trebuie să fie mai întâi familiarizat cu formula exponentiation de bază sau cel puțin le-au la îndemână.

Produsul puterilor cu aceeași bază - în acest caz, baza de calcul, precum și gradul de adăuga până

Împărțind puteri cu aceeași bază - baza de rezervă, gradul de scădere

Construcția gradului de putere - să prezinte gradul paranteze, astfel, multiplicat

Produsul în măsură - dezvăluie paranteze, cu fiecare factor fiind construit în acest grad

Împărțirea în grade - dezvăluie parantezele, cu numărătorul și numitorul construiesc în acest grad

Apoi, amintiți-vă regula de bază pentru reducerea fracției:

pentru a reduce fracția pentru a găsi cel mai mare divizor comun al numărătorul și numitorul, iar apoi se împarte numărătorul și numitorul prin acel număr.

Acum, se taie cu fracțiune de grade, de exemplu, la întrebarea dumneavoastră.

Folosind formulele de mai sus se convertesc numărătorul și numitorul

și acum pentru a reduce fracția este un pic: 0.01 Răspuns

Pentru a reduce o fracție cu un grad nu a fost o problemă pentru tine, trebuie să cunoască proprietățile gradului:

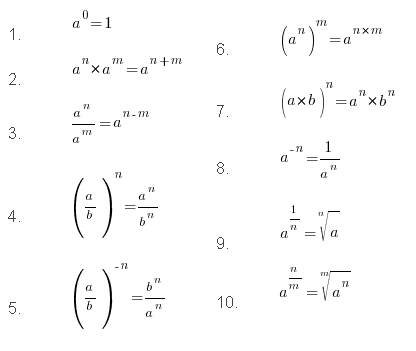
Acum, în scopul de a consolida cunoștințele, să luăm în considerare câteva exemple.

Este necesar să se reducă o fracție:

Motive grade dezordine pe cărămizi - care este, aveți nevoie pentru a ridica astfel de numere, care sunt atât numărătorul și numitorul, și apoi să prezinte toate gradele de aceste foarte bine. În acest caz, 2 și 3 (2 * 3 = 6, 2 ^ 2 = 4). Solutia este:

În primul rând, trebuie să înțeleagă în mod clar regulile. Sunt doar 4.

1) La înmulțirea grade diferite de același număr, se adaugă exponenți. De exemplu: ^ 2 * 3 3 ^ 4 = 3 ^ (2 + 4) = 3 ^ 6.

2) La împărțirea diferitelor grade de același număr, exponenții se scad. De exemplu:

3) Odată cu construirea nivelului de putere, exponenții sunt multiplicate. De exemplu: (2 ^ 3) ^ 4 = 2 ^ (3 * 4) = 2 ^ 12.

4). La scoaterea rădăcinilor gradelor de numere, exponent împărțit la indicele rădăcinii. De exemplu: √ (5 ~ 8) = 5 * (8/2) = 4 ^ 5.

Acum, soluții concrete. 4 este un 2 la puterea a doua. Prafuri ^ 8 = 4 (2 ^ 2) ^ 8 = 2 ^ 16. Doi la puterea a doua ridicat la a opta putere a doua va fi în gradul XVI.

^ 16 * 2 2 ^ 2 = 2 ^ 18. În numărătorul avem 2 ^ 18.

Numitorul diferitelor grade de 5 și 16. Dar 16 este de 2 la puterea a patra, adică, = 2 ^ 16 4. Apoi ^ 5 = 16 (2 ^ 4) ^ 5 = 2 ^ (4 * 5) = 2 ^ 20. Deci, la numitor, avem 5 ^ 2 * 2 ^ 20. Iar numărătorul și numitorul poate fi redus cu 2 ^ 18. Numărătorul rămâne 2 ^ (18-18) = 2 ^ 0 = 1, iar numitorul 2 ^ (20-18) = 2 ^ 2. Asker: 1 / (5 * 2 * 2 * 2). Dacă se dorește, acesta poate fi transformat după cum urmează: 1 / (5 ^ 2 * 2 ^ 2) = 1 / (25 * 4) = 1/100. Acest lucru este posibil și complet, dar dacă se dorește, pot fi convertite și: = 1/10 ^ 1/100 2 = 10 ^ 0/10 ^ 2 = 10 ^ (0-2) = 10 ^ (- 2). Dar acest lucru nu este necesar.

Totul va fi foarte simplu, dacă ne întoarcem la proprietățile cunoscute (caracteristici) ale fracțiuni cu un grad.

După cum putem vedea, ecuația propusă trebuie extins, astfel încât să se aloce aceeași bază, apoi în funcție de adăugare de acțiune sau scade gradul corespunzător.

Mai jos este invitat să facă referire la o soluție din acest exemplu.

Este cel mai simplu de a explica cu un exemplu.

Să presupunem că avem nevoie să taie aici această fracțiune:

În primul rând, avem nevoie pentru a găsi numere care ar fi constituită atât numărătorul și numitorul. În acest exemplu, aceste numere sunt 2 și 3. (2 * 3 = 6; 2 * 2 = 4).

utilizând proprietățile fracțiilor, putem face astfel de transformări:

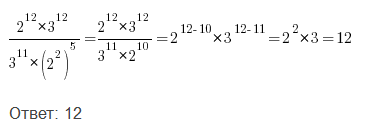
Lucrarea este în documentele de examen la matematică. Aici analiza unul dintre exemple:

Pentru a reduce fracțiunea la nivelul necesar pentru a rupe baza puterii de astfel de numere, care ar fi în numitorul și numărătorul, și să introducă fracția noastră sub forma unor noi puteri ale acestor numere. După aceea folosim proprietățile fracțiilor, în scopul de a reduce fracțiunea de un grad.

Nu este nevoie să ne amintim că fracțiunile cu aceleași puteri, vom adăuga și scade în multiplicarea prin divizarea.

În exemplul nostru, reducerea fracțiilor pot să apară după cum urmează:

În replică el a primit 0,01.

Pentru a reduce o fracțiune de grad, este necesar să se cunoască următoarele reguli:

1) Atunci când înmulțirea numere identice cu grade diferite, gradul necesar pentru a adăuga;

2) La împărțirea numerelor identice grade diferite, gradul necesar pentru a scădea;

3) La efectuarea gradelor de construcție în măsură exponenți trebuie înmulțite;

4) La efectuarea extracției de măsură rădăcină necesară pentru a diviza un indice exponent în rădăcină.

De exemplu, avem nevoie să profite de primele două reguli:

^ 8 * 4 2 ^ 2/5 ^ 2 * 16 ^ 5 = 4 ^ 9/5 ^ 2 * 4 ^ 10 = 1/5 ^ 2 * 4 = 1/100 = 0,01