Cum de a găsi matricea Adjoint

Cofactori - este unul dintre conceptele de algebra matrice aplicate elementelor matricei. Găsirea cofactori este una dintre acțiunile algoritmului de determinare a matricei inverse și diviziunea funcționare matrice.

Matricea algebră este nu numai cele mai importante secțiuni ale matematici superioare, dar, de asemenea, un set de metode pentru diverse aplicații prin elaborarea unui sistem de ecuații liniare. Matricea utilizată în teoria economică și în construcția de modele matematice, cum ar fi programarea liniară.

Algebră liniară descrie și analizează mai multe operații pe matrice, inclusiv însumării, înmulțire și împărțire. Acest din urmă efect este condiționată, este de fapt o multiplicare cu matricea inversă la a doua. Și apoi du-te la ajutorul cofactori elementelor matricei.

Noțiunea de adăugiri algebrice decurge direct din celelalte două definiții fundamentale ale teoriei matricei. Acesta este principalul factor determinant și minor. Determinant unei matrice pătratică este un număr care se obține prin următoarea formulă bazată pe valorile elementelor: Δ = a11 • a22 - a12 • A21.

Matricea minoră - este determinant său, al cărei ordine este unul mai puțin. Minor orice element obținut prin eliminarea din numerele rândurilor matricei și coloanelor poziției elementului respectiv. Ie Minor M13 este echivalentă cu determinantul matricei obținută după ștergerea primului rând și a treia coloană: M13 = a21 • a32 - a22 • A31.

Pentru a găsi o matrice adăugări algebrice, este necesar să se determine minorul corespunzător elementelor sale cu un anumit semn. Semnul depinde de ce poziție ar trebui să elementul. În cazul în care cantitatea de numere de linie și coloană - un număr par, atunci cofactor este un număr pozitiv, în cazul în care ciudat - negativ. Ie: Aij = (-1) ^ (i + j) • Mij.

Primer.Vychislite cofactori.

Matrix numit tabel care constă din valorile definite, și având o dimensiune în n coloane și rânduri m. Sistemul de ecuații algebrice liniare (SLAE) de ordin superior pot fi rezolvate prin matricea sa asociat - sistemul de matrice și matricea expandat. Primul este o matrice A coeficienți de sistem ale variabilelor necunoscute. Când adăugați la această matrice coloana matrice B se obține membri SLAE liberi matrice extinse (A | B). Construcția matricei expandat este una dintre etapele din soluția de ecuații arbitrare.

În general, sistemul de ecuații liniare pot fi rezolvate prin substituție, ci pentru sisteme liniare de mari dimensiuni astfel de calcul este foarte consumatoare de timp. Și în acest caz, folosesc adesea legate de matrice, inclusiv extensii.

Înregistrarea unui anumit sistem de ecuații liniare. Bețivan transformarea ei prin aranjarea factorilor în ecuațiile, astfel încât aceleași variabile necunoscute în sistem strict aranjate una deasupra celeilalte. ratele de liber, fără transferul necunoscut la o altă parte a ecuației. Atunci când rearanjarea termenilor și ia în considerare transferul de semnul lor.

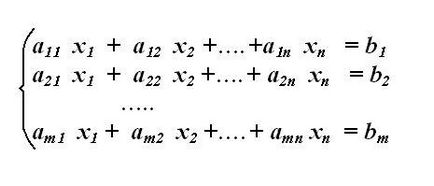
Se determină matricea sistemului. Pentru această listă separată coeficienții variabilelor necunoscute Slough. Necesitatea de a scrie în aceeași ordine în care apar în sistem, și anume, prima ecuație a primului coeficient stabilit în primul rând și prima coloană a matricei. Ordinea rândurile matricei corespunde noii ordini a sistemului de ecuații. Dacă unul dintre necunoscutele în sistemul de ecuații este offline, atunci coeficientul său este egal cu zero - zero, de umplere într-o matrice pe poziția de linie. Matricea sistemului rezultat trebuie să fie pătrat (m = n).

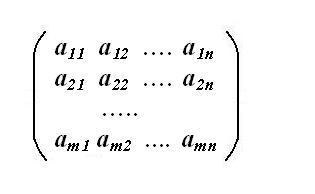
Găsiți matricea augmentată a sistemului. Factori liberi în ecuațiile sistemului familiar al egalității scrie într-o coloană separată, păstrând aceeași ordine de rânduri. Într-o matrice pătrată din dreapta liniei verticale a pus toți coeficienții. Mai jos adăugați coloana rezultată a termenilor liberi. Aceasta va fi mărită matricea dimensiune inițială SLAE (m, n + 1), unde m - numărul de rânduri, n - numărul de coloane.

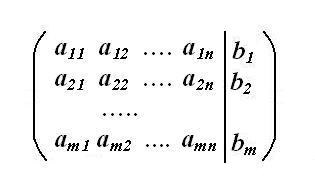
Este pentru matricea extinsă prin metoda Gauss calculează rădăcinile unui sistem de ecuații algebrice liniare. Gauss este una dintre cele mai activ utilizate metode de rezolvare a ordinii liniare ridicată.

• matrice sistem extins