Cum de a găsi centrul de greutate al triunghiului 1
mai multe segmente pot fi împărțite într-un triunghi arbitrar, a cărei lungime este necesară pentru calcularea cel mai des. Aceste segmente de puncte situate în nodurile triunghi centrele laturile sale, la centrele cercurilor inscriptionare circumscrise de legătură, dar și pentru alt punct important al geometriei triunghiului. Anumite variante de realizare a calcula lungimea acestor segmente în geometria euclidiană sunt prezentate mai jos.
Dacă segmentul pe care doriți să căutați, se conectează oricare două noduri ale oricărui triunghi, este una dintre laturile figurii geometrice. Dacă se cunoaște, de exemplu, lungimea celelalte două laturi (A și B) și unghiul pe care îl formează (y), lungimea acestui segment (C), puteți calcula pe baza teorema cosinusului. Fold pătratelor lungimile laturilor, scade rezultatul din cele două părți de aceeași lungime, înmulțit cu cosinusul formei unghi, iar apoi obține rădăcina pătrată din valoarea rezultată: C = √ (A² + b²-2 * A * B * cos (γ)).
Dacă o linie începe la unul din vârfurile triunghiului, se termină pe partea opusă și este perpendicular pe ea, atunci acest segment se numește înălțimea (h). Acesta poate fi găsit, de exemplu, cunoașterea zonei (S) și o lungime (A) a părții pe care este coborâtă înălțimea - diviza de două ori zona de lungimea laturii: h = 2 * S / A.
În cazul în care segmentul care leagă mijlocul de fiecare parte a oricărui triunghi de sus și situată vizavi de această parte, numele acestui segment al mediana (m). Găsiți lungimea sa poate fi, de exemplu, cunoscând lungimile laturilor (A, B, C) - plieze patratele dublat lungimilor a două laturi, se scade din valoarea obținută pentru patratul laturii în mijlocul căreia capetele tăiate, și apoi a obține rădăcina pătrată a unui sfert din rezultatul: m = √ ((2 * A² + 2 * b²-C²) / 4).
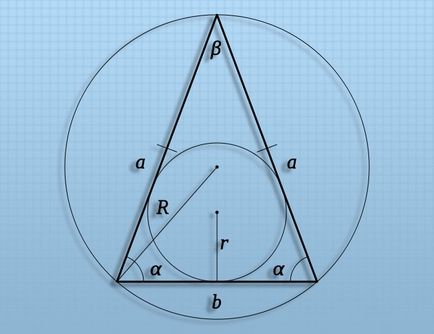
Dacă o linie care leagă centrul cercului inscris la un triunghi arbitrar, iar oricare dintre punctele de cerc tangente cu laturile triunghiului, apoi găsiți lungimea prin calcularea razei (r) a cercului inscris. În acest scop, de exemplu, se împarte aria (S) a triunghiului în perimetrul său (P): r = S / P.
Dacă o linie care leagă centrul cercului circumscris despre un triunghi arbitrar, cu oricare dintre nodurile figurii, lungimea sa poate fi calculată prin găsirea raza cercului circumscris (R). Dacă se cunoaște, de exemplu, lungimea unei laturi (A) într-un triunghi și unghiul (α), situată ea opusă, pentru a se calcula lungimea intervalului dorit, împărțiți lungimea părții la dublul sinusul unghiului: R = A / (2 * sin (α )).
Mediana unui triunghi - un segment care leagă vârful triunghiului cu punctul de mijloc partea opusă. Într-un triunghi echilateral, mediana bisects și înălțimea simultan. Astfel, segmentul dorit poate fi construit în mai multe moduri.

Folosind un conducător și un creion împarte latura unui triunghi echilateral în jumătate. Petreceți un segment care conectează punctul și a găsit colțul opus al triunghiului. În același mod retrase din circuitul agricol următoarele două segmente. Desenați mediana unui triunghi echilateral.
Desenați înălțimea unui triunghi echilateral. Cu ajutorul gon picătură perpendicular pe vârful unui triunghi pe partea opusă. Ați construit înălțimea unui triunghi echilateral. Este atât mediana ei.
Construirea bisectoarea unui triunghi echilateral. Orice unghi de triunghi echilateral este egal cu 60º. Atașați un echer la o latură a triunghiului, astfel încât punctul de referință coincide cu vârful triunghiului. Una dintre părți trebuie să treacă exact prin contor, cealaltă parte să traverseze semi-cerc la punctul cu marca de 60 °.
Notă punct de diviziune în 30º. Petreceți o grindă care leagă punctul găsit și vârful triunghiului. Găsiți intersecția razelor X din partea laterală a triunghiului. Segmentul rezultat este bisectoarea unui triunghi echilateral, care este mediana acestuia.
În cazul în care un triunghi echilateral înscris într-un cerc, trasează o linie dreaptă care unește partea superioară a acesteia cu centrul cercului. Marcați punctul de intersecție al acestei linii cu partea a triunghiului. Segmentul care leagă vârful triunghiului și lateral pentru a fi mediana triunghiului echilateral.
Construirea bisectoarea unghiului a poate fi un triunghi echilateral cu o busolă. Pentru a construi aceste două cercuri cu centrul la celelalte două vârfuri ale triunghiului și o rază egală cu latura triunghiului. Cercurile se intersectează în două puncte la vârful unghiului a la punctul N. conecta aceste puncte împreună. Ai construit o bisectoare a unghiului a.
centru de piese pot fi găsite în mai multe moduri, in ciuda ceea ce este deja cunoscut datele de pe ea. Este necesar să demontați constatarea centrul cercului, care este setul de puncte, care sunt situate la o distanță egală de centru, deoarece această cifră - una dintre cele mai comune.
