Cum de a găsi baza trapezului

Pentru a stabili un astfel de patrulater, un trapez ca și trebuie să fie determinată pentru cel puțin trei laturi. Prin urmare, de exemplu, este posibil să se ia în considerare problema, în condițiile în care specifică lungimea diagonalelor unui trapez. și unul dintre vectorii laterali.

Condițiile Figura problemei este prezentată în Figura 1. în acest caz, se presupune că cele de mai sus trapezoid - un AVCD patrulater, în care lungimea predeterminată a diagonalele AC și BD, precum și o parte laterală AB, reprezentată de vectorul a (ax, ay). Datele sursă primite ne permit să găsim două osnovaniyatrapetsii (atât de sus și de jos). Într-un exemplu specific baza inferioară a AD va fi găsit mai întâi.

Luați în considerare triunghiul ABD. Lungimea laturii sale AB este egală cu magnitudinea unui. Să | o | = sqrt ((ax) ^ 2 + (ay) ^ 2) = a, atunci cosf = ax / sqrt (((ax) ^ 2 + (ay) ^ 2) ca direcția cosinusul unui let specificat. p are o lungime diagonală de BD și AD dorit lungime s. Apoi, prin cosinusul, p ^ 2 = a ^ 2 + x ^ 2-2axcosf. sau 2-2axcosf x ^ + (a ^ 2-p ^ 2) = 0 .

Soluțiile ecuației pătratice: X1 = (2acosf + sqrt (4 (a ^ 2) ((cosf) ^ 2) -4 (a ^ 2-p ^ 2))) / 2 = acosf + sqrt ((a ^ 2) ((cosf) ^ 2) - (a ^ 2-p ^ 2)) == un ax * | sqrt (((ax) ^ 2 + (ay) ^ 2) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + p ^ 2) = AD.

Pentru a găsi baza superioară soare (lungimea în găsirea unor soluții de asemenea desemnate x) folosit modul | a | = a, iar a doua diagonală BD = q și cosinusul unghiului ABC, care este în mod clar egal cu (p-p).

Următorul este considerat triunghiul ABC, care, ca și mai înainte, aplicat teorema cosinus și există următoarea soluție. Având în vedere că cos (n, p) = - cosf, bazat pe soluția la AD, putem scrie următoarea formulă prin înlocuirea p cu q: BC = - o * ax | sqrt (((ax) ^ 2 + (ay) ^ 2 ) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + q ^ 2).

Această ecuație este un pătratică și, respectiv, are două rădăcini. Astfel, în acest caz, este de a selecta numai rădăcinile, care au o valoare pozitivă, deoarece lungimea nu poate fi negativă.

PrimerPust trapez ABCD în partea laterală AB este dată de vectorul a (1, sqrt3), p = 4, q = 6. Găsiți osnovaniyatrapetsii .Reshenie. Folosind algoritmi derivate de mai sus pot fi scrise: | a | = a = 2, cosf = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (sqrt (13) +1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2.

Trapez considerat un patrulater în care cele două părți sunt paralele, celelalte două nu. Înălțimea trapezului este numit un segment tras perpendicular între două linii paralele. În funcție de datele brute poate fi calculată în diferite moduri.

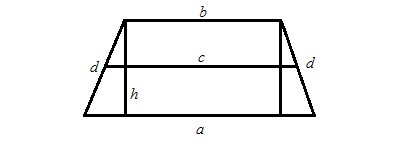
• Baze fete Cunoștințe linia mediană trapezoidală, precum și, opțional, zona și / sau perimetrul acesteia.

O modalitate de a calcula aria trapezului este produsul înălțimea și linia de mijloc. Să presupunem că există un trapez isoscel. Apoi înălțimea unui trapez isoscel cu bazele a și b, aria S și perimetrul P se calculează după cum urmează:

h = 2 x S / (P-2 x d). (A se vedea. Figura 1)

Dacă numai o zonă cunoscută de trapez și baza sa, formula de calcul înălțime poate fi derivată din zona = 1 / 2h x formula trapezoid S (a + b):

Să presupunem că este un trapez cu aceleași date ca și în figura 1. înălțimea de 2 tragerea la sorți, obținem un dreptunghi ale cărui două laturi mai mici sunt picioarele triunghiuri dreptunghiulare. Notăm role mai mici pentru x. Se găsește împărțind diferența dintre lungimile bazelor mari și mai mici. Apoi, prin teorema lui Pitagora pătrat din înălțimea egală cu suma pătratelor ipotenuzei și piciorul d x. Preluați rădăcina acestei sume și pentru a obține înălțimea h. (Fig. 2)

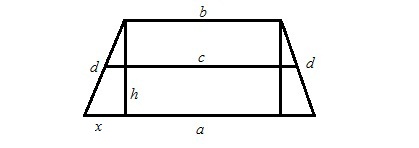
O figură matematică cu patru unghiuri se numește trapez, în cazul în care cuplul este pe laturile sale opuse paralele, iar cealaltă pereche - nr. laturi paralele numit osnovaniyamitrapetsii. celelalte două - parte. Într-un trapez rectangular unul din colțurile de la marginea - line.

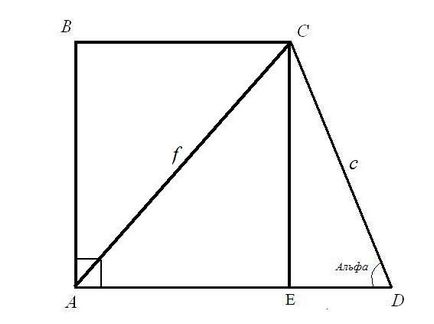
Sarcina 1.Locate bază BC și AD trapezoid dreptunghiular. dacă știm lungimea diagonala AC = f; laterale lungime CD = c și un unghi de la ADC său = α.Reshenie: Luați în considerare un triunghi dreptunghic CED. Cunoscute ipotenuza c și unghiul dintre ipotenuzei și EDC picior. Ia fete lungime CE si ED: unghiul de formula CE = CD * sin (ADC); ED = CD * cos (ADC). Deci: CE = c * sinα; ED = c * cosα.

Luați în considerare un ACE triunghi dreptunghic. Ipotenuză AC și piciorul CE știi, pentru a primi partea AE de regula unui triunghi dreptunghic: suma pătratelor picioarelor este egală cu pătratul ipotenuzei. Deci: AE (2) = AC (2) - CE (2) = f (2) - c * sinα. Se calculează rădăcina pătrată pe partea dreaptă. Ați găsit baza superioară a trapez dreptunghiulare.

Lungimea bazei AD este egală cu suma lungimilor a două segmente AE și ED. AE = rădăcină pătrată (f (2) - c * sinα); ED = c * cosα) .Itak: AD = rădăcina pătrată (f (2) - c * sinα) + c * cosα.Vy găsită bază inferioară dreptunghiular a unui trapez.

Sarcina 2.Locate bază BC și AD trapezoid dreptunghiular. dacă știm lungimea diagonala BD = f; laterale lungime CD = c și un unghi de la ADC său = α.Reshenie: Luați în considerare un triunghi dreptunghic CED. Găsiți lungimea laturilor CE și ED: CE = CD * sin (ADC) = C * sinα; = CD * cos ED (ADC) = c * cosα.

Luați în considerare un ABCe dreptunghi. Prin proprietatea dreptunghiului AB = CE = c * sinα.Rassmotrite triunghi ABD. Prin proprietatea triunghi pătratul ipotenuzei este egal cu suma pătratelor celorlalte două laturi. Prin urmare, AD (2) = BD (2) - AB (2) = f (2) - c * sinα.Vy găsită bază inferioară a trapezoid dreptunghiular AD = rădăcină pătrată (f (2) - c * sinα).

Prin dreptunghi regula BC = AE = AD - ED = rădăcină pătrată (f (2) - c * sinα) - * cosα.Vy a găsit cu baza superioară a trapez rectangular.

Mai mică bază trapezului este paralelă cu una dintre laturile sale având lungimea minimă. Calculați această valoare în mai multe moduri, folosind unele date.

Dacă știți lungimea celor două - o bază mare a trapezului și linia de mijloc - utilizată pentru a calcula cea mai mică bază de proprietate trapez. Potrivit acestuia, linia de mijloc este identică cu jumătate din baza de trapez. În acest caz, cea mai mică bază este egală cu diferența de două ori lungimea liniei mediane și lungimea bazei mari a figurii.

Dacă astfel de parametri sunt cunoscuți trapezoidal ca suprafață, înălțime, lungimea bazei mari, calculul mai mica baza figurii pentru a conduce aria baza formulei trapez. În acest caz, rezultatul final obținut prin scăderea din diferența de două ori secțiunea privată și înălțimea unui astfel de parametru ca lungimea bazei trapez mare.

Lungimea cea mai mică parte a unui trapez dreptunghiular este calculată printr-o metodă diferită. Acest parametru este egal cu produsul din lungimea celei de a doua parte și sinusul unghiului ascuțit la acesta accumbens. În aceste cazuri, atunci când unghiul este necunoscut, cea mai mică parte a echivalat cu înălțimea trapezului și se calculează folosind teorema lui Pitagora. Cea mai mică parte a unui trapez dreptunghiular găsi folosind teorema cosinusului: s² = a² + b²-2ab * cosα; unde a, b, c reprezintă laturile triunghiului; α este unghiul dintre laturile a și b.