Construirea bisectoarea unghiului

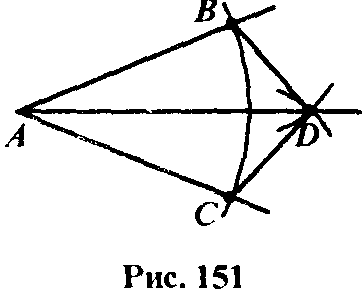
Din vârful A al unghiului ca centru al cercului care descrie raza arbitrară (Fig. 15). Fie B și C - punctul de intersecție cu laturile unghiului. Din punctele B și C descrie un cerc de rază una. Fie D - punctul de intersecție, altele decât o jumătate de normă AD este bisectoarea unghiului A. Să ne dovedesc acest lucru. Pentru aceasta considerăm triunghiurile ACD și Avd. Ele sunt pe trei laturi. Acest lucru implică faptul că unghiurile corespunzătoare DAV și DAS, și anume fascicul AD împarte în jumătatea unghiului BAC și, prin urmare, este bisectoarea.

5. Prin acest punct trage o linie dreaptă perpendicular pe o anumită linie.

Să-un punct O și o linie a. Există două cazuri:

1) punctul O se află la linia A;

2) punctul O se află pe linia chinta.

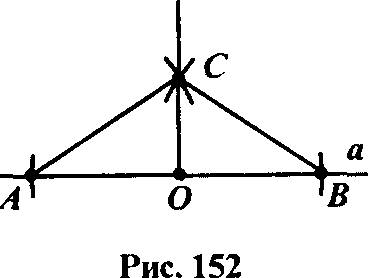
În primul caz, construcția este aceeași ca și în problema 4, deoarece perpendiculara din punctul O situată pe linie, - un unghi drept bisectoare (fig.16.).

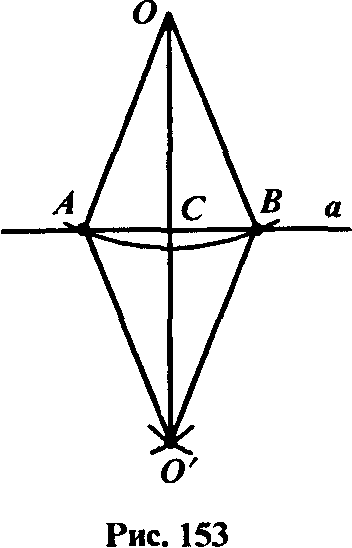
În al doilea caz din punctul O ca centru al unui cerc este desenată care intersectează linia a (fig. 17), iar apoi de la punctele A și B din aceeași rază dețin două mai multe circumferențial. Să O „- punctul de intersecție, care se află în semiplanul, diferit de cel care conține punctul O. Direct 00“ este perpendiculară pe această linie a. Să ne dovedesc acest lucru.

Notăm prin intersecția liniilor AB și OO“. Triunghiurile AOB și AO'V sunt pe trei laturi. Prin urmare, unghiul egal cu unghiul CCA O'AS și, prin urmare, triunghiuri O'AS CCA și egal pe ambele părți și un colț între ele. Prin urmare, colțurile lor ASO și ASLO sunt egale. Deoarece unghiurile sunt adiacente, ele sunt drepte. Astfel, sistemul de operare este, perpendicular pe linia A.

9. Conversia forme geometrice. Conceptul de transformare

Obiectivul principal este de a valida geometria normelor de construcție a cifrelor cu proprietăți dorite. Dar construcția folosim conceptul de egalitate a cifrelor, care se poate determina prin conceptul de transformare.

Să presupunem că o anumită cifră F și fiecare punct al F atribuit la un singur punct în plan. Setul de puncte care sunt asociate cu punctele de F F este o figură „în general diferită de R. spus că cifra P“ obținută prin transformarea R. forme pot fi de asemenea, a spus că modelul P „este imaginea F pentru conversie, iar cifra P - prototipul F“.

În cazul în care A „- punctul de cifra P“ care corespunde punctului A din F, atunci vom spune că o „- imaginea punctul A și punctul A - imaginea inversă a lui A“.

Conversia studiat în geometrie sunt în general reciproc fără echivoc, adică cele în care diferite puncte ale figurii corespund diferitelor imagini. Cel mai simplu caz transformărilor bijective - o transformare în care fiecare punct O cifră inserată în potrivirea același punct, adică, mod de F este ea însăși figura. Această transformare se numește transformarea identității.

Luați în considerare exemplele de schimbare cifre.