Clasa de fizică și matematică
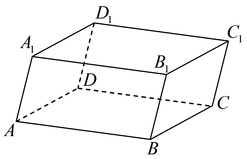
Se numește prismă paralelipiped a cărei bază este un paralelogram.
Paralelograme, care este alcătuit dintr-o cutie, numit fețele sale. partea lor - coaste. și vârfurile de paralelogram - top box. În toate aspectele cutiei - paralelogram.
Paralelipipede, ca orice prismă, poate fi directă și oblică.
De obicei, distinge oricare două fețe opuse și numite bazele lor. iar cealaltă parte - fețele laterale ale cutiei. Muchiile paralelipipedul, nu fac parte din motivele menționate, ca și marginile laterale.
Două față a cutiei, având o muchie comună, a spus să fie adiacente. și care nu au margini comune - opus.
Segmentul care leagă două noduri care nu aparțin de o fata, numita diagonala a cutiei.
paralelipiped directă, a cărei bază este dreptunghiul este numit un paralelipiped dreptunghic. In toate fațetele unui cuboid - dreptunghiuri.
Lungimea la margini paralele ale unui paralelipiped dreptunghiular sunt numite dimensiunile liniare (dimensiuni). În cuboid trei dimensiuni liniare.
Fața opusă a cutiei sunt egale și paralele.Pătratul diagonalei paralelipiped dreptunghic este egală cu suma pătratelor trei dimensiuni.