Care este indicele de refracție al sticlei și când este necesar să se cunoască

Aceste numere sunt necesare în cazul în care doriți să determine indicele de refracție al sticlei în raport cu alte medii.

Ce alte valori sunt utilizate pentru rezolvarea problemelor?

reflexie totală. Se observă atunci când trecerea luminii dintr-un mediu mai dens la o mai puțin densă. Aici, atunci când o anumită valoare a unghiului de incidență refractie are loc la unghiuri drepte. Aceasta este, diapozitivele fascicul de-a lungul graniței dintre cele două medii.

Limitarea unghiului de reflexie totală - este valoarea minimă la care lumina nu merge în mediu mai puțin dens. Mai puțin el - este refractată, și mai mult - o reflectare a aceluiași mediu, din care se deplasează lumina.

Sarcina № 1

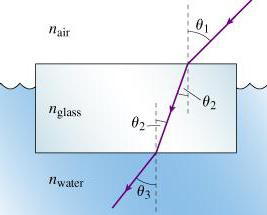
Stare. sticlă indicele de refracție are o valoare de 1,52. Este necesar să se determine unghiul de limitare la care lumina este reflectată în totalitate de suprafețele de interfață: sticlă și aer, apă și aer, cu sticla de apa.

Trebuie să utilizați datele pentru indicele de refracție al apei dat în tabel. El aer una.

Decizia în toate cele trei cazuri se reduce la calcule prin formula:

păcat α0 / păcat β = n1 / n2. unde n2 se referă la mediul din care se propagă lumina și n1 care penetrează.

Litera desemnată unghi prag α0. Unghiul p este de 90 de grade. Adică, este o unitate de sine.

Pentru primul caz: α0 păcat = 1 n sticlă /. întrucât unghiul limită este egal cu sinusul inversă a 1 / n al sticlei. 1 / 1,52 = 0.6579. Unghiul este 41,14º.

În al doilea caz, în determinarea arcsinusul trebuie să substituie valoarea indicelui de refracție al apei. Fraction 1 / n apă va valoarea1 unghi / 1,33 = 0 7519. Acest arcsinus 48,75º.

Al treilea caz este descris de raportul apă de sticlă n și n. Necesitatea de a calcula arcsinusul pentru fracția: 1,33 / 1,52, adică, numărul de 0875. Găsiți valoarea unghiului de limitare la arcsinus sale: 61,05º.

Raspuns: 41,14º, 48,75º, 61,05º.

Problema № 2

Stare. Vasul este imersat cu prisma de sticla de apa. indicele său de refracție este de 1,5. Baza prismei este un triunghi dreptunghic. Piciorul mai mare este perpendicular pe partea de jos, iar al doilea - este paralelă. Un fascicul de lumină în mod normal, incidente pe fața superioară a prismei. Care ar trebui să fie mai mic unghi dintre o cateta orizontală și ipotenuza, astfel încât lumina a atins piciorul dispus perpendicular pe fundul vasului, și a lăsat prisma?

Pentru fasciculul apărut din prisma în acest mod trebuie să scadă sub unghiul limită la fața interioară (cea care, în secțiunea transversală a prismei este ipotenuza triunghiului). Acesta este unghiul de limitare egală cu construcția dorită colțului unui triunghi dreptunghic. Din se obține legea refracției luminii că sinusul unghiului maxim împărțit la sinusul de 90 de grade, egal cu raportul dintre doi indici de refracție: apă la sticlă.

Calculele conduc la o astfel de valoare pentru unghiul de limitare: 62º30' .