Calcularea derivatelor
Motto: Unul a întrebat: „Care este diferă derivate din produsul?“ „Derivatele sunt studiază în clasa de matematică, iar produsul - o literatură lecție“ - urmată de răspunsul studentului.
În epigraful descris situația reală a practicii mele. Problema a apărut atunci când pupila încurca funcțiile regulilor de diferențiere, în special, este în măsură să determine produsul derivat al două funcții. Pentru a evita o astfel de interpretare a acestui articol pentru a vă reaminti că noi facem doar matematică, și aici, termenul „produs“ înseamnă rezultatul înmulțirii, și „derivat“ este limita a raportului funcției creștere cu creșterea argumentului, atunci când acesta din urmă tinde la zero. Procesul de calcul se numește derivat diferențiere.
Derivatele funcțiilor elementare prin definiție, adică prin limita se calculează o singură dată, la o prelegere (în clasă) pentru a fixa derivatul de conectare și o limită. În viitor, ne interesează doar în aplicarea practică a acestui concept, astfel încât să se calculeze derivata sunt formule și reguli de diferențiere a funcțiilor gata făcute.
Aici ne uităm la modul în care să și cum nu pentru a calcula derivatele, dar, din păcate, mulți studenți și chiar studenți fac.
Cum de a calcula derivați
Este scris peste tot, în toate manualele și pe o varietate de site-uri în rețea.Pentru a găsi derivați, este necesar, folosind una sau o altă sursă, să învețe încă Formula diferențiere a funcțiilor elementare. De exemplu, a se vedea un articol detaliat pe masa derivate și primitivelor. Pentru mai complexe decât tabular, funcțiile combinate ale regulilor de calcul al derivatului sumei, produsul, fracția. Expresiile matematice corespunzătoare ca puteți găsi oriunde. Dar, în opinia mea, regulile de diferențiere a funcțiilor mai bine să definească și să memoreze cuvintele:
- Un factor constant poate fi luat ca semn al derivatului.
- Derivata o sumă egală cu suma derivatelor.
- Produsul derivat este egal cu „derivat din primul factor înmulțit cu al doilea derivat plus al doilea factor înmulțit cu primul“.
- Derivatul a fracțiunii este egală cu „un derivat al numărătorului înmulțit cu numitorul, minus derivatul numitorului, înmulțit cu numărătorului împărțită la numitor în piață.“
- Derivata funcției compozit este derivata funcției exterioare, înmulțită cu derivatul din interiorul și calculat „continuarea“ la masă.
Cum să nu calculeze derivați
- În primul rând, nu este necesar să se complice simplu.
- A nu se confunda termenii și factorii (sumă și de produs).
- A nu se confunda puterea de-Xa și securea funcție exponențială.
- Nu trebuie să uităm că derivata unei funcții compozit este evaluată „continuarea“ până la o formulă de tabel.
- Nu fi timid pentru a pune între paranteze.
In cele mai multe dintre următoarele exemple ilustrează realizări derivați de calcul în care
1. Calculele sunt efectuate foarte slab. cu erori evidente;
2. Dreptul, dar nu a fost optimă. și anume lung și cu o eroare probabilă în lipsa de concentrare;
3. destul de bine.
Notă cu privire la regula pe care am pus numărul unu.
În cazul în care lucrarea este unul dintre factorii este constantă, atunci nu este necesar să se folosească regula de lucrări derivate. Mai mult decât atât, nu este necesar de a face acest lucru, deoarece este adesea însoțită de o astfel de eroare de operare. Un factor constant poate fi luat ca un semn al derivatului!
Dacă o fracțiune numărătorul sau numitorul este constantă, atunci nu este necesar să se folosească regula pentru fracțiuni derivate. Această acțiune în elevi și studenți mai adesea însoțite de erori. Un factor constant poate fi luat ca un semn al derivatului!
Cea mai frecventă eroare în aceste exemple - de a uita pentru a pune bara (denumirea derivatului) a numărului, sau să-l pună, și „nu a văzut“ acțiunea următoare, și anume, nu ia în considerare faptul că constanta derivat (număr) este egal cu zero.
Aici, pentru primul și al treilea exemplu de simplitatea și calitatea abordării consolelor c impunerea unui factor numeric este evidentă. Dar nu este atât de clar pentru al doilea exemplu, în cazul în care numitorul este o funcție trigonometrice. Mai mult decât atât, sunt de acord că, pentru acei studenți care posedă funcții complexe derivat rău (regula 5), mai preferat în acest exemplu poate fi regula pentru fracția diferențiere.
Cu toate acestea, pentru o serie de alte funcții, mai ales pentru puterea, trebuie doar numitor „rândul său,“ în numărătorul și rădăcinile - în parte pentru că, în acest caz, putem folosi cele mai simple și cu formula tabular cele mai memorabile (x # 945; ) = # 945; x # 945; - 1.
În aceste două exemple, prezentate erorile uzuale în diferențierea fracției cu o constantă, iar în exemplul următor, este necesară trecerea de la rădăcină la putere fracționată, deoarece altfel adesea uitat că o astfel de funcție nu este o masă și trebuie să fie diferențiate în funcție de regula pentru funcțiile compozite.
diferențiere pe termen constant cu adus la zero-constant factor în diferențierea este menținută.
Mai mult, pentru un motiv oarecare, mulți elevi derivate din functia y = x 2 + 0,1 mai ușor de calculat decât același tip de derivat (0,1 + x 2)“. Iar pentru derivata funcției y = 0,1 × 2 realizeze adesea existența primei reguli, și pentru (x 2 x 0,1) „nr.
Atunci când face acest tip de greșeală, amintiți-vă că permutarea suma nu este schimbat, iar permutarea factorilor nu se schimba produsul. Rearanjarea-le ca preferați, și se aplică ușor primul sau al doilea reguli de derivare.
În primul caz, variabila este în baza gradului, am citit: „X la puterea unui“. În al doilea - o variabilă în exponent, am citit, „și puterea X“. Caracteristici formule diferite pentru calcularea derivatelor diferite. Cm. Tabel.
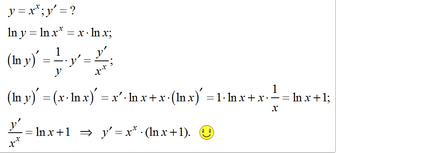
Aceasta este o funcție complexă care nu este direct legată de orice clasă de putere, nici o demonstrație de clasă. Pentru a calcula derivata în astfel de cazuri, este adesea necesară pentru a produce o conversie preliminară. De exemplu, prima expresie este logaritmul, luând apoi derivații din ambele părți ale variabilelor sale, și în cele din urmă a ajuns la o ecuație pentru a găsi derivatul dorit al variabilei x.
funcții complexe, această funcție nu este direct dependentă de variabila specificată, și de la alte funcții. Cu alte cuvinte, valoarea sa nu poate fi calculată într-un singur pas. De exemplu, functia y = sinx2 și y = sin 2 x sunt complexe. Să vedem cum sunt calculate valorile lor, de exemplu, atunci când x = 2.
Pentru o funcție y = sinx2 trebuie mai întâi ridicate într-un pătrat x 2 2 = 4, și apoi pentru a calcula valoarea sinus a 4-dx. Facem acest lucru folosind un calculator: sin4 = -0,75680249530792825. ≈ -0,76 (nu uitați că funcțiile trigonometrice de argumente sunt considerate ca fiind date în radiani).
Pentru o funcție y = sin 2 x, determină mai întâi sinusul-2 folosind calculatorul: sin2 = 0,9092974268256816. și apoi erecte valoarea în păcat pătrat 2 2 = (0.9092974268256816.) 2 = .82682181043180595. ≈ 0,83.
Astfel, vom calcula mai întâi valoarea funcției interne și apoi folosi ca argument la exterior.
Conform celui de al cincilea regula de diferențiere, pentru a determina necesitatea de a face derivat opusul - mai întâi pentru a calcula derivata funcției exterioare argumentului său, și apoi înmulțim cu derivatul din interior.
Așa cum am menționat, cel mai adesea greșeli în această operațiune. Greșelile pot fi foarte diferite, următoarele trei comune.
Greseala 1) Nu se poate aplica doar regula drept, „nu menționând“ că funcția complexă.
În următoarea formulă și puterea de diferențiere a funcțiilor trigonometrice utilizate nu secvențial, dar în același timp, un derivat incorect calculat într-un singur pas.
2a eroare) nu poate da seama în cazul în care funcțiile interne și externe în cazul în care.
În exemplul următor, exponentul este deasupra x. și anume Argumentul de mai sus, prin urmare, gradul funcției sinus intern și extern. Discipolul a luat oricum, am decis că sinusul la pătrat și a făcut o greșeală.
Pentru a scapa de acest tip de eroare, să învețe să analizeze funcții complexe pentru a separa interiorul din exterior, trebuie doar să urmăriți ordinea în care ați efectuat calcule, și diferențierea în ordine inversă. Este posibil să se aranjeze parantezele lipsă, și în cazul în care încă se confruntă cu dificultăți, de a introduce notația suplimentare. În ceea ce privește gradul, vă puteți aminti acest lucru - cu privire la modul reprezintă desemnarea exponent, care este baza sa (este ridicată).
Exemplul 12.
Se utilizează la sfârșitul sinusul trigonometrice a dublei formula unghi, pentru a înregistra răspunsul în forma sa cea mai compactă.
Exemplul 13.
Aici, la sfârșitul factorilor de asemenea, rearanjate pentru a scrie răspunsul într-o formă mai compactă și ușor de citit.
A treia eroare) Regula nu este utilizată până la sfârșitul anului
După ce se ia în considerare faptul că funcția este complexă și va fi suficient. Și în cazul în care funcția este încorporat de mai multe ori? De exemplu, rădăcina pătrată a sumei logaritmilor două baze diferite, dintre care unul depinde de sinx. iar al doilea de COSX. Sau tangenta cu arc, în funcție de logaritmul natural, care este, la rândul său, depinde de x pătrat.
Exemplul 14.
Exemplul 15.
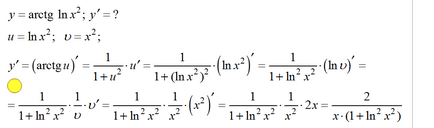
Exemplul anterior demonstrează modul în care prin introducerea unor simboluri suplimentare. Dar, în opinia mea, nu este încă cel mai bun mod pentru calcule lungi. Cea mai bună abordare pentru diferențierea unei funcții compozit - consolelor, care se pot construi pe în mod clar sau cel puțin să consolideze abilitatea de a imagina mental.
Noi aranja parantezele și dezvăluie treptat în afara lor la interior. Conținutul următoarelor paranteze este variabilă asupra căreia derivarea formula fu „· (u)“. fu Derivata „găsi derivați ai mesei, înlocuind în formula x la u. Dacă este făcută corect, procesul este finalizat prin faptul că conținutul acesteia din urmă, suporturile intime coincid complet cu una din tabelul de formule pentru derivații.
